Lesson Two -- Activity
In the previous activity you created a design using straight line segments and
converted your design to a set of ordered pairs . As you noticed each line
segment was
created by connecting two points . These line segments have a characteristic
(when looked
at in their positions in your design) that we call steepness in English. In
algebra there is a
concept which is equivalent to steepness in English and that is the SLOPE. In
this
activity you find the slopes of the line segments from the design you created in
the
previous activity. Notice that as you move from one point to another on the
coordinate
plane your position with respect to the origin changes; in other words, there
will be
HORIZONTAL and/or VERTICAL changes. In algebra we find the slope of the line
segment created by moving from one point to another on the coordinate plane by
dividing
the VERTICAL change by the HORIZONTAL change.
SLOPE = VERTICAL CHANGE / HORIZONTAL CHANGE
Example
In this 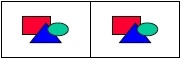 design the
slope of the line segment from the
design the
slope of the line segment from the
point (0,3) to the point (2,4) is calculated as:
Slope = (4 - 3)/(2 - 0) = 1/2.
Find the slope of all the line segments in your design
( remember division by zero is
not allowed and a non zero number divided by zero equals zero):
Lesson Three -- Objective:
o Write linear equations in the form: y = mx + b
Textbook correlation:
McDougal Littell Algebra 1, chapter 3 section 3.4 and 3.5; exercise 18 0n page
123
and 26, 27 on page 129.
Resource Materials:
o Graph paper and pencil
o Graphics calculator
o Ruler
Lesson Three -- Activity
A: In the previous activities you created a design using straight line segments
and converted your design to a set of ordered pairs. Then, you found the slopes
of the line
segments from the design you had created. In this activity you will find an
equation for
each of the line segments which slopes you calculated in the previous activity.
An (linear)
equation is a rule which shows the relation between the vertical and horizontal
coordinates of points on a line. For example, (1,3) and (2,5) are on a line
whose equation
is y = 2x + 1. In general, the form of the equations you will write will be: y =
mx + b
where m is the slope and b is a number on the y -axis at which the segment (or
the
extension of the line segment) crosses the y-axis.
Example
First write the general form of a linear equation: y = mx + b. Then, find the
slope
(remember you calculated this before). Finally, you use the coordinates of one
of the
points to find b.
In this
 design the slope of
the line segment from the
design the slope of
the line segment from the
point (0,3) to the point (2,4) is calculated as:
m = Slope = (4 - 3)/(2 - 0) = 1/2. Next, we write the general formula with
the
calculated slope substituted for m : y = (1/2)x + b. Then, we substitute the
coordinates of (0,3) for x and y, and solve for b :
3 = (1/2) 0 + b, so we have 3 = b and the equation is: y = (1/2)x + 3. Notice
that if you
apply this rule to the x coordinates of both (0,3) and (2,4), you will have the
corresponding y coordinates.
Find an equation for all the line segments in your
design ( how would you deal with
undefined and zero slopes?).
| FIRST POINT |
SECOND POINT |
FORMULA y = mx + b |
EQUATION |
| |
|
|
|
| |
|
|
|
Lesson Four -- Objective:
o Write linear equations in the form: y = mx + b (by the use of a
calculator)
Textbook correlation:
McDougal Littell Algebra 1, chapter 3 section 3.4 and 3.5; exercise 18 0n page
123
and 26, 27 on page 129.
Student Resource Materials:
o Graphics calculator
o The work from previous activity
o The movie Twister
In the previous activities you created a design using
straight line segments and
converted your design to a set of ordered pairs. Next, you found the slopes of
the line
segments from the design you had created. Then, you found an equation for each
of the
line segments which slopes you had calculated in the previous activity. In this
activity
you check your work with a graphing calculator. The calculator will calculate m
and b for
you! Carefully read the example below and then, fill in the chart that follows .
Example
In this
 design I calculated
the slope of the line segment
design I calculated
the slope of the line segment
from the point (0,3) to the point (2,4) and found an equation for the line which
passes
through the given points as follows::
Slope = m = (4 - 3)/(2 - 0) = 1/2. Next, we write the general formula with
the
calculated slope substituted for m: y = (1/2)x + b. Then, we substitute the
coordinates of (0,3) for x and y, and solve for b:
3 = (1/2) 0 + b, so we have 3 = b and the equation is: y = (1/2)x + 3. Notice
that if you
apply this rule to the x coordinates of both (0,3) and (2,4), you will have the
corresponding y coordinates.
Now, I want to check my work with a graphing calculator. Here is how I do it
with a
TI-82: Press STAT and then ENTER (EDIT should be highlighted before you press
ENTER). Enter 0 and 2 in L1 and 3 and 4 in L2
 , then press STAT,
, then press STAT,
right arrow key, number 5 (LinReg(ax+b)), and finally ENTER twice. You will
see  . Here a is your m and b is your b and if
the points you entered in
. Here a is your m and b is your b and if
the points you entered in
L1 and L2 lie on a line, r will be equal to 1.
Check all the eqautions you found in the previous activity:
EQUATION YOU
CALCULATED |
CALCULATOR'S
EQUATION |
ERRORS (IF
ANY) |
| |
|
|
| |
|
|
Teachers Resources
| Book Name |
Author |
Publisher |
| Symmetry |
Hermann Weyl |
Princeton University Press,
Princeton, New Jersey |
Mathematics , the science of
patterns |
Keith Devlin |
Scientific American Library |
North American Indian
Designs |
Eva Wilson |
British Museum Press |
Integrating Educational
Technology Into Teaching |
M.D Roblyer; Jack
Edwards; Mary Anne
Havriluk |
Prentice Hall |
| Algebra 1 textbook |
|
McDougal Littell |



