1 What this Assignment is About
I have kept revising this assignment and never posted it.
It has now turned into a mixed bag with
some NLE and the beginning of SLE. No Maple programming for this one, although,
you should
probably do a bit of prototyping, and of course I expect you do do some
validation for what you
implement in C++ or Java.
2 Nonlinear Equations
2.1 The Newton-Raphson and secant algorithms
This should be fairly straightforward. Again, I am not
asking you to implement these algorithms in
Maple, only in Java/C++. You already wrote code for the validation for the
previous assignment ,
so just reuse for this one.
2.2 A small application
In this application you will learn how to define a 1D
function based on a 2D (or, more generally,
nD) function.
2.2.1 The context of the problem
This is just a variation on the theme of the bouncing ball from the previous
assignment, only this
time our terrain is described by a 2D “elevation” function:
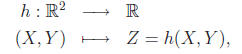
where Z = h(X, Y ) is the elevation at (X, Y ).
A mortar is installed at coordinates (X0, Y0) on the
map. Therefore the mortar really occupies
a 3D point at coordinates
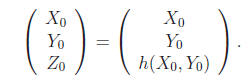
Our mortar fires a shell with an initial speed vector
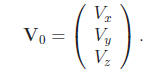
The Z component of this initial speed vector is assumed to be positive . You may
if you want
specify this speed vector in spherical coordinates (2 angles and a magnitude) if
this facilitates your
understanding of the underlying geometry of the problem, but this will have no
impact on the
numerical solution .
2.2.2 What you have to do
Determine the coordinates of the impact point of the mortar’s shell.
2.2.3 For extra credit (10 pts)
Replace the mortar by a more pacific kind of gun, say one of these training
machines that shoot
tennis balls. Of course, you don’t earn the extra 10 pts just by replacing all
references to “mortar”
and “shell” by “tennis ball” in your Maple worksheet and report: You now have to
handle multiple
bounces as you did in the previous assignments.
2.2.4 Go from nD to 1D
It is really straightforward to write the equation for the trajectory of the
shell in 3D. At time
0 ≤ t ≤ timpact, the shell occupies the 3D point of coordinates
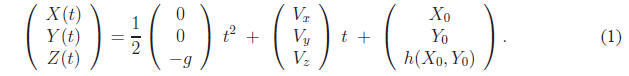
The point of impact, when t = timpact, lies on the surface defined by the
elevation map:
Z(timpact) = h (X (timpact) , Y (timpact)) . (2)
If you substitute for X (timpact) and Y (timpact) in Equation (2) using the
equation of the trajectory
Equation (1), then you can get a nonlinear equation with a single unknown,
timpact,
f(timpact) = 0.
This is the 1D nonlinear equation that you must solve.
3.1 The csc350lib.linalg.base package/namespace
What you will do for this assignment is to implement the basic Matrix class and
its two subclasses
ColumnVector and RowVector. I have decided to implement the two vector classes
as subclasses of the Matrix class because that way we only have to implement one
method for
matrix product.
CSC 350 – Fundamental of Mathematical Computation , Assignment 03 02/28/2009 3
We are only going to implement matrix product, addition, and transposition.
Special matrices (e.g.
diagonal matrices) will be produced by static functions/methods of the Matrix
class rather then
being implemented as a subclass. The main interest of having, say, a
DiagonalMatrix class or
an IdentityMatrix class is that it can speedup a lot matrix product or
transpose . You could
achieve a similar effect by storing in the Matrix class a set of boolean
variables providing additional
information about your matrix (e.g. isSymmetric, isDiagonal, isOrthogonal,
etc.). You have studied these two alternative class designs as “inheritance” vs.
‘composition” (or
“is a” vs. “has a”). I think that in the case of matrix classes, the latter is
generally preferable, but
this is largely a matter of taste.
Anyway, the main purpose of storing information about the type of matrix we are
dealing with
is to speedup matrix product, transpose, and inversion. Because we are only
mostly interested in
solving general SLEs, I will spare you the hassle of handling all the special
cases (assuming that
dimensionsmatch adding or multiplying two symmetricalmatrices produces a
symmetricalmatrix,
same for diagonal matrices. What about orthogonal or block matrices?).
4 Evaluation
4.1 What to hand in
For this assignment, you have to hand in your C++ or Java implementation, your
Maple validation
worksheet, and as usual a report discussing your implementation choices and
results, and the
limitations of the methods implemented.
B: You should hand in printouts of your (complete)Maple worksheet and of your
report on the day
the corresponding part of the assignment is due.
The maximum number of points is 100, but extra points could be awarded for
excellent aspects of
the project or report. The point distribution for this assignment is as follows:
C++/Java Code
Accomplishes what was demanded 25 pts
Good class design 10 pts
General quality & readability 10 pts
Maple validation
Accomplishes what was demanded 15 pts
Comments and analysis 10 pts
Report
Discussion and analysis of the results 20 pts
General quality of the writing and presentation 10 pts
4.3 Various point penalties
Hopefully we won’t have to apply many of these:
| Project folder incomplete or not properly cleaned
up |
-5 pts |
| Report file missing from the project folder |
-5 pts |
| Maple file missing |
0 for that part |
| Late penalties |
| Printed copy of the report, 1 day late |
-5 pts |
| Project folder (uploaded to EnVision server), per
day late |
-5% |
if you submit a project late, then it is your responsibility to notify the TA
(with CC. to me) that the
project is finally available for download on the EnVision server. If you fail to
do so, then the “late
penalty clock” will keep ticking until the TA gets around to checking your
folder on the EnVision
server and notices your project. Unless asked explicitly to do so, do not mail
your project folder
as an attachment.
As I explained in class, I will post sometimes partial solutions to the
assignments , to make sure
that nobody gets too far behind. Obviously, it will be impossible to get any
point on a part after a
solution for it has been posted (this does not affect the late penalty count).



