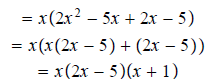Factoring Polynomials of the Form ax^2+bx+c

Chapter 8.3-- Factoring Polynomials of the form
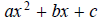
Factoring polynomials of the form 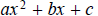is usually done in one of two ways .

Part 1 Factoring by trial (and error)

Given the trinomial find the factors of both a and c . Then check to see which products of these factors add up to b .

Question 7: Factor
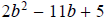
Factors of

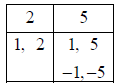
Now test all the combinations of binomial pairs (until you get one that works).

In this case the last one we tried worked. We could have shortened our trials if we noticed that since the middle term of the problem is negative, we wouldn't have to test the positive factors .

Question 6 Now you try this one:
Factors of

Now test all the combinations of binomial pairs (until you get one that works).

The answer is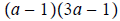

Question 53: Factor

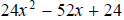
Take out the common factor first:

The factors are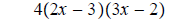

Question 38: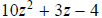

So the factors are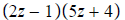

Part 2 Factoring by grouping

Algorithm: In the trinomial multiply ac . Then find all the factors of ac .Find the pair r,s that add up to b , and rewrite the trinomial as .  Finally factor this by grouping .

Question 78: Factor

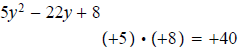
All the factors of 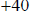are:
1,40 sum is 41
2,20sumis22
4,10 sum is 14
5,8 sum is 13
I used "sum" because the last coefficient is positive
Use minus because the middle coefficient is negative

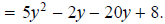
Now factor by grouping:
 

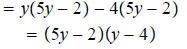
Question 71 Now you do this one: Factor
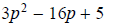
ac = 15
Write down all the factors of ac =15
1,15 their sum is 16 (This is what we want.)
3,5 their sum is 8

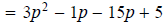
factor by grouping.

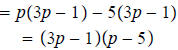
Question 107: Factor
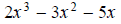
Factor out the common factor first:

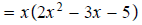
Multiply 2 and 5
Factors of 10 are
1,10 their difference is 9
2,5 their difference is 3