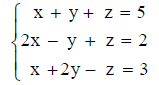• A matrix is a rectangular array of numbers , enclosed in
brackets . The numbers are called the
entries of the matrix. Entries are identified by their row and column position.
Rows run
horizontally, columns run vertically.
• Examples :
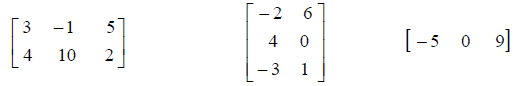
• An augmented matrix can be used to represent a system of
equations.
The system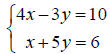 
is represented as
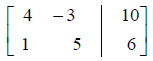
Notice that equation 1 becomes row 1, equation 2 becomes
row 2, the x terms are in column 1, the
y terms are in column 2, and the equal signs are represented by the vertical
line .
• Write the augmented matrix that represents the following
system of equations.
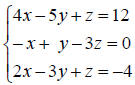
• Write the system of equations that corresponds to the
following augmented matrix.
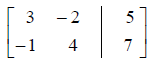
• Write the system of equations that corresponds to the
following augmented matrix.
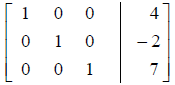
• To solve a system of equations using its augmented
matrix representation, we will transform the
original augmented matrix into a form similar to the previous example . This will
allow us to read
the solutions of the system .
• There are three row operations that can be applied to an
augmented matrix. These correspond to
algebraic operations that can be applied to the corresponding system of
equations.
• Row operations
1. Interchange any two rows .
2. Replace any row by a nonzero constant multiple of that row .
3. Replace any row by the sum of that row and a constant multiple of another
row.
• Matrix method - an example.
Solve
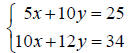
Step 1 : Write the augmented matrix.
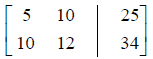
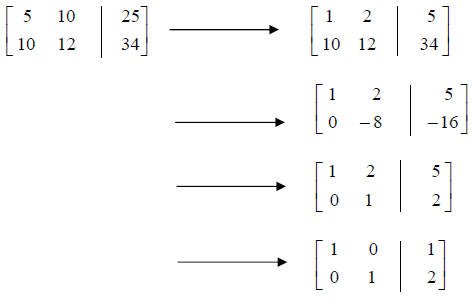
Step 2 : Use row operations to transform the augmented
matrix into the form
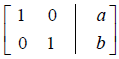
which has solutions x = a, y = b .
The last augmented matrix corresponds to the system
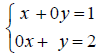
which has solution x = 1, y = 2.
Check :
5(1) + 10(2) = 25
10(1) + 12(2) = 34
• The strategy for transforming the original augmented
matrix using row operations:
1. Place a 1 in row1, column 1
2. Place 0's in all other entries in column 1 - leaving the 1 in row 1, column 1
unchanged
3. Place a 1 in row 2, column 2
4. Place 0's in all other entries in column 2 - leaving the 1 in row 2, column 2
unchanged
5. Continue this pattern. Place a 1 in row n, column n. Place 0's in all other
entries of column n -
leaving the 1 in row n, column n unchanged.
6. If a row is obtained that contains only 0's to the left of the vertical bar,
place it at the bottom of
the matrix.
A matrix generated using the strategy outlined above is
said to be in row-echelon form.
• Solve by writing the augmented matrix in row-echelon
form.
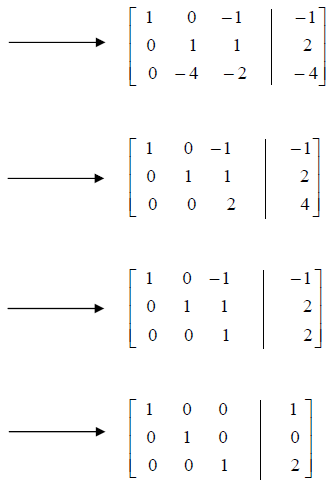
The solution is x = 1, y = 0, z = 2 .
• Example of an inconsistent system.
Solve
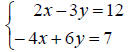
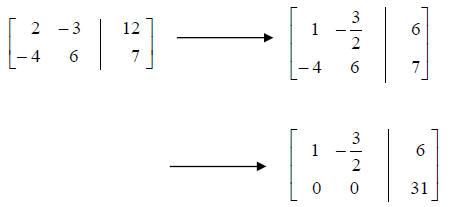
Notice that row 2 corresponds to the equation 0 = 31, a
contradiction. Therefore, this
system has no solution. It is inconsistent.
• Example of a consistent system with dependent equations.
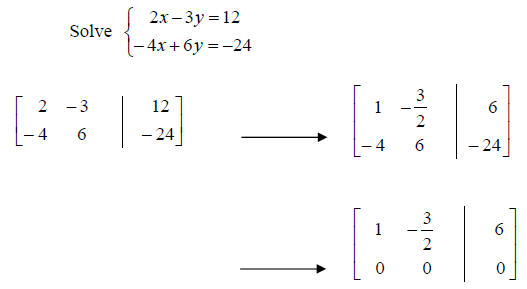
Notice that row 2 corresponds to the equation 0 = 0, an
identity. This indicates that
equation 2 can be derived from equation 1. They are equivalent equations .
Any point on the line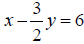 
is a solution of the system.
Solutions: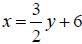 
where y is
any real number . ( y is called a parameter.)
Give three different solutions for this system.
• Use the matrix method to solve the following system.
