Fractions
Any fraction can be represented in many ways. Consider the fraction 1/2 .
The number 1/2
represents one part of a whole that is divided into two equal pieces:
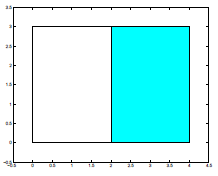
1/2 of the above rectangle is shaded. The same rectangle
can be divided again so that it is
broken into 4 pieces:
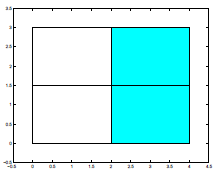
The same area is shaded, but now we have two out of four
or 2/4 of the rectangle shaded.
It is clear, then, that 1/2 and 2/4 are equal. Similarly, we could have taken
the same rectangle
and cut it into six equal pieces:
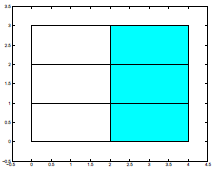
We still have exactly half ( 1/2) of the rectangle shaded,
but now there are three of the six
equal pieces shaded. So 1/2 and 3/6 are equal. We could cut this rectangle into
any number
of equal pieces and then shade half of them, and each one would give us another
way to
represent 1/2 . Some other ways are 5/10, 22/44, 500/1000, 37/74. Notice that in
each case,
the denominator (that is, the bottom number) is twice as large as the numerator.
The
simplest way to write this particular fraction is 1/2 because the numerator and
denominator
don’t have any factors in common other than 1. When you are asked to reduce a
fraction,
your goal is to write the fraction this way. To do this, you simply divide the
numerator
and denominator by the same number until there are no common factors left.
Dividing (or
multiplying) the numerator and denominator of a fraction by the same number does
not
change the value of the fraction .
Example 1: Reduce 3/15
Since 3 and 15 are both divisible by 3, we can divide the
top and bottom of this fraction to
get 1/5 .
Example 2: Reduce 24/32
Since 24 and 32 are both divisible by 2, we can divide the
top and bottom to get 12/16. Notice,
though, that this fraction is not reduced completely : the numerator and
denominator still
have factors in common. Since 12 and 16 are both divisible by 4, we can divide
the top and
bottom to get 3/4 . 3 and 4 don’t have any factors in common, so we’re done. Of
course, 24/32
could be reduced in one step simply by dividing the top and bottom by 8 to get
3/4.
Multiplication and Division of Fractions
Multiplying fractions is the simplest of operations to perform because it is
worked exactly
the way one might guess: multiply the tops and multiply the bottoms.
Example 3: Perform the following multiplications
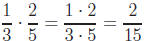 The symbol · represents
multiplication.
The symbol · represents
multiplication.
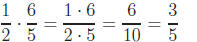 Notice that this
fraction needed to be reduced.
Notice that this
fraction needed to be reduced.
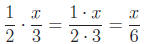 x is treated just like
any other number.
x is treated just like
any other number.
Dividing fractions is almost as simple as multiplying fractions, but the
operation requires
one extra step. First take the reciprocal of the fraction that you are dividing
by, and then
multiply.
Example 4: Perform the following divisions:
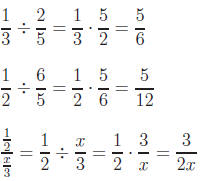
Addition and Subtraction of Fractions
Addition and subtraction of fractions takes a little more
finesse than multiplication and
division. To add two fractions, the fractions must have the same denominator. We
already
know that if we divide the top and bottom of any fraction by the same number the
value of
the fraction does not change (we saw this when we reduced fractions). We can
also multiply
the top and bottom by any number ( except zero , of course) and it won’t change
the value
of the fraction. This fact is used to do fraction addition and subtraction.
Example 5: Perform the following addition and
subtraction:
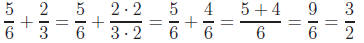
First we get a common denominator by multiplying the
numerator and denominator of the
second fraction by 2. Once we have a common denominator, we add the numerators
and
keep the denominator.
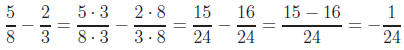
Subtraction works exactly the same way as addition. Here
we had to change both denominators.



