Take Home Quiz (Real Numbers)
(1) Given x > 0 and y < 0 determine the sign of y (y - x)
and
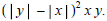Also, if x - y > 0 then
determine the sign of
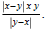
(2) Express the statement as an inequality :
The absolute value of x - 3 is greater than 8 and less than 16.
(3) Express
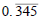as a fraction and then express
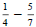as a repeating decimal .
(4) Using the Properties of the Real Numbers, solve the
equation 4 x = 7 x - 3.
Take Home Quiz ( Exponents and Radicals )
(1) Simplify
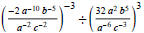
(2) Simplify
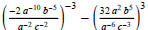
(3) Simplify
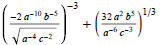
(4) Simplify
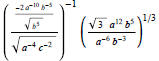
(5) Given
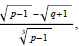rationalize the denominator .
(6) Given
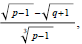rationalize the numerator .
(7) Given
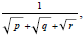rationalize the denominator .
Take Home Quiz ( Quadratic Functions )
(1) Express
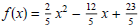in the form
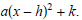Sketch the graph of f and label the x and y intercepts, the
zeros, the vertex , and the line of symmetry.
(2) Given constants b and e, express
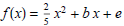in the form
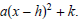Sketch
the graph of f and label the
x and y intercepts, the zeros , the vertex, and the line of symmetry.
(3) Given
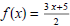and
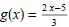find
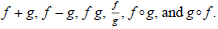
(4) Solve the equation
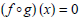given
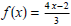and
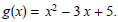
(5) Determine the domain of
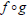given
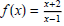and
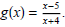Justify your statement.
Take Home Quiz (Properties of Division)
(1) Use long division to divide
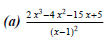
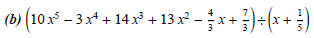
(2) Use synthetic division to divide
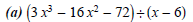
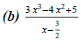
(3) Express the function in the form
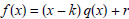for the given value of k, and demonstrate that
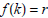
(a) f (x) = -4 x3 + 6 x2 + 12 x + 4 with
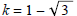
(b) f (x) = -3 x3 + 8 x2 + 10 x - 8 with
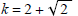
(4) Find a real number k such that x - 3 is a factor of
x 4 - 5 x3 - k x2 + 18 k + 18.
(5) Find the values for k such that f (x) = k2 x3 - 4 k
x + 3 is divisible by the linear polynomial x - 1.
(6) Show that x - k is not a factor of f (x) = -x4 - 3
x2 - 2 for any real number k.
(7) Construct a cubic polynomial function with
x-intercepts of 1, 2, and 3 which passes through the point (4, 12).
Take Home Quiz (Functions)
(1) Determine a so that the lines 2 x - 3 y = 9 and x - 3
y = -11 are parallel.
(2) Determine a so that the equation through the points
(a, 3) and
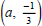is 2 x - 4 y = -11.
(3) Determine a so that the equation through the points
(a, 3) and (-a, 4) is x + 6 y = 21.
(4) Given f (x) = 2 x2 + 3 x - 4 find
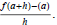
(5) State the domain and range of the function
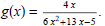
(6) State the domain of the function
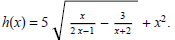
Take Home Quiz (Inverse Functions)
(1) Determine whether the following functions are
one-to-one.
(a) f (x) = x2 + 4
(b) f (x) = 2 x3 - 4
(c) f (x) = -54 + 54 x - 15 x2 + 2 x3
(d)
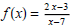
(2) Determine whether or not the given functions are
inverses of each other or not.
(a) f (x) = x3 - 4 and
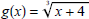
(b) f (x) = x2 + 5, x ≤ 0 and
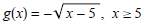
(3) Find the inverse of the given function, it if exists.
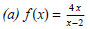
(b) f (x) = (1x3 + 1)5
(c) f (x) = x2 - 6 x, x ≥ 3
Take Home Quiz (Exponential and Logarithmic Functions )
(1) True or False? For those which are true if the domain
is restricted, give the domain; for those that are false, give the
correct equality.
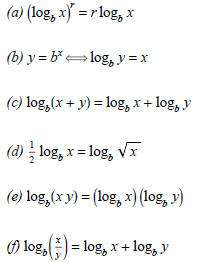
(2) (Exponential and Logarithmic Equations) Solve the
following equations for real x and give the number of solutions
you find for each one. Also clearly state any extraneous solutions that you find
for each one .
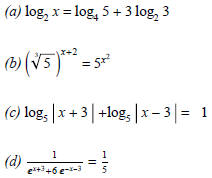
(3) (Modeling Population) Based on the estimate that there
are 10 billion acres of land of Earth, and that each acre can
produce enough food to feed 4 people, some demographers believe that the Earth
can support a population of no more
than 40 billion people. The population of the Earth reached approximately 5
billion in 1986 and 6 billion in 1999. If the
population of the Earth is growing according to the formula
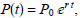where
t is the time after the population is P0
and r is the growth rate, when will the population reach the theoretical limit
of 40 billion?
