Visualizing Newton's Method on Fractional Exponents

Nils B. Lahr
128 Elliott Drive, Menlo Park, CA 94025 USA
Clifford A. Reiter
Department of Mathematics, Lafayette College, Easton PA, 18042 USA

Abstract -- Newton's method for finding complex solutions of the equation z^α −1 = 0 is
investigated for real values of α. The bifurcations that occur as the power α varies are illuminated
using computer graphics. In particular, the appearance of an attracting 2-cycle just below even
powers is investigated .

Keywords
Visualization - Chaos - Newton's method

Introduction
Computer graphics allows the visualization of the dynamics of iteration in powerful ways. Pictures
of bifurcations of functions of a real variable and of basins of attraction for complex dynamics play
an important role in understanding the dynamics of both real and complex iteration — from period
doubling to chaos; for examples, see [1-5, 9-12, 14]. This short note describes bifurcations in the
complex dynamics of Newton's method that we can visualize using a sequence of images.

Visualizing the convergence of Newton's method in the complex plane has been the subject
of much recent study. Often those images show the basins of attraction of Newton's method applied
to a polynomial of low degree . Typically, a family of third degree polynomials is considered or
zⁿ −1 for n equal to 3, 4 or 5 is considered. Also, in [8] Newton's method on systems with 2
complex variables is considered. In [15] nonintegral exponents are considered and in [13] a
generalization of Newton's method is discussed. The dynamics of direct iteration of z^α + c for
fractional exponents , which generalize the classical Mandelbrot and Julia sets, are described in [6]
and are analyzed in [7]. Instead of direct iteration, we consider the bifurcations that occur using
Newton's method on z^α −1 as we vary α .

Consider the basins of attraction for the roots of z³ −1 compared to those for z⁴ −1. The
first has three main basins of attraction around the three roots of unity with symmetric turbulence on
the boundaries. The second case is quite similar except it contains four basins of attraction. In
general, we expect that slight changes to α should produce only slight changes in the behavior of
Newton's method on z^α −1. However, it is clear that some fundamental changes in behavior must
occur as we change from three to four basins of attraction. Thus, the question of how the change
from three to four basins occurs is of interest. How many basins of attraction are there for any given
positive real α? Does every starting guess converge to a root? Where do the bifurcations occur?
This paper takes a look at those questions. Figs. 1-8 show the convergence of Newton's method on
z^α −1 for 3 ≤α ≤ 5 . Fig. 1 shows three basins of attraction and Fig. 5 shows four basins of
attraction as described above.

The Computation
Newton's method for solving f (z) = 0 begins with an initial guess 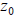and proceeds via:
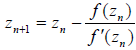. Here the function is f (z) = z^α −1 so this simplifies into
.
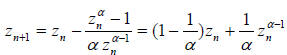Notice that the second version of this formula can be evaluated more quickly since it involves only
one power of a complex number. Also notice we can think of steps of Newton's method as iteration
of the function 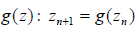where .

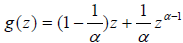In all the figures the initial guess 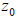used for Newton's method corresponds to position in the
picture and varies with 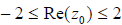and 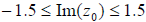. The color used indicates the
basin of attraction and the shade indicates the iteration count modulo 3. For example, all the shades
of green indicate convergence to the root 1. The shades are chosen so that when we are within the
green basin we are moving in the direction of increasing iteration count if we move from the darkest,
through the medium, and to the lightest shade.

All the images were computed with extended precision floating point arithmetic using 19-20
significant digits and using high precision exponents so that the range of magnitudes is .
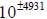Complex exponentiation was implemented using the standard branch cut along the negative real
line . A sequence, 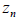, was considered convergent if successive values differed by less tha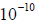n in
magnitude. The roots were dynamically determined with a distance of discrimination of 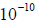. The
roots and 2-cycles discovered can be independently verified as described in the next section.

Results
In Fig. 1 we see three symmetric basins of attraction that are expected when α = 3 since the roots of
z³ −1 are the three roots of unity. In Fig. 2, α = 3.3 and the turbulent region between the left-most
basins increases in size. Notice also that unlike the case when α = 3 there are boundaries between
the red and blue basins where there is no turbulence (look at some of the small red and blue regions
near the negative real axis).

In general the equation z^α −1 = 0 will have roots 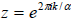where k are integers so that
2πk /α is in the interval (−π ,π ] . That is, if k ranges over the integers satisfying
−α / 2 < k ≤α / 2 the values for z given above run through the roots. The three roots that are
observed when α = 3.3 correspond to k = 0, ±1. These are 1 and approximately − 0.327 ± 0.945i .
The roots for other α's can also be computed this way.

When we increase α to α = 3.88221 there are still only three roots but there is severe
turbulence. The V-shaped turbulent region between the primary red and blue regions seen in Fig. 3 is
larger than that in Fig. 2 and almost forms a "basin" of its own. In the first two figures the maximum
number of iterations required for convergence was 66. In this figure the maximum number of
iterations required for determining any pixel was 152,931. However, for every pixel computed the
algorithm did eventually converge to one of the three roots!

A striking bifurcation occurs with a very slight increase to α = 3.88222 . Fig. 4 shows three
basins of attraction in red, green and blue and a large region in yellow where Newton's method does
not converge. However, in this region, Newton's method approaches an attractive 2-cycle. In the
long term, values shown in yellow oscillate between values close to r = −0.883623 + 0.154366i
and s = −0.883623 − 0.154366i . No pixel required more than 1855 iterations to converge to a root
or to find the 2-cycle in this figure.

Using Mathematica^TM it is easy to check numerically that r and s are 2-cycles since they are
roots to the equation h(z) = z where α = 3.88222 , h(z) = g(g(z)) , and g(z) was defined in the
previous section. Now the fact that this is an attractive 2-cycle can be verified since
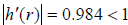and likewise for s. Going back to the case when α = 3.88221 we can find roots
to h(z) = 0 given approximately by u = −0.881416 + 0.154395i and v = −0.883228 − 0.156458i ;
notice the roots u and v are not quite conjugates. These roots also form a 2-cycle, but the 2-cycle is
just barely repelling since 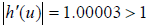and likewise for v. The fact that this derivative is just
barely over one explains why such a large number of iterations were required for computing some
pixels in Fig. 3.

The appearance of an attractive 2-cycle continues as α increases toward 4 but the points in
the 2-cycle approach each other and the negative real axes. At α = 4 , shown in Fig. 5, these points
meet at -1 and form an attractive basin shown in magenta. Any small increase in α produces yet
another basin of attraction. In Fig. 6, where α = 4.1, a cyan basin of attraction is conjugate to the
magenta basin. Notice that there is no turbulence on the negative real axis which is a boundary
between these basins. Also notice the fractal cyan and magenta "arches". As α increases turbulence
does appear on the negative real axis. At first it is restricted to inside the unit circle. Between
α = 4.7 and α = 4.8 the turbulence moves out along the negative real axis. Fig. 7 shows the basins
of attraction when α = 4.8. Notice that there is almost a five-fold symmetry. Finally, the expected
five-fold symmetry appears in Fig. 8 where α = 5.

In Fig. 9, the angle of the long term behaviors is shown verses the power α for 1 ≤α ≤ 11.
The angle is the angle about the origin from the positive real axis. Attractive roots are shown in blue
and attractive 2-cycles are shown in green. Notice that just before α equals each even integer there is
an attractive 2-cycle. The points in the 2-cycle become less distinct and approach -1; that is, the
angles approach ±π . At the even integer, the 2-cycle has become the new root at -1. As soon as α
increases beyond the even integer, the root at -1 splits into two attractive roots. These roots move
apart as α increases and become uniformly spaced around the unit circle when α reaches the next
higher odd integer. The most striking feature in this figure is the sudden appearance of the attractive
2-cycles. The first few values of α where these bifurcations occur can be computed: 1.8163832,
3.882214033, 5.893141755, and 7.897747821.

The sequence of images in this paper shows chaotic behaviors not usually seen in images of
the convergence of Newton's method. The intertwining basins with smooth boundaries observed
just above α = 4 are a result of the branch cut used in computing the complex exponential function.
Those smooth boundaries do not occur for Newton's method on zⁿ −1 with integer exponents.
There are also fascinating bifurcations that occur just below even integers. Attractive 2-cycles
appear for those exponents. The changeover of a 2-cycle from repelling to attractive near
α = 3.88221 can be analyzed as well as observed visually.

Authors' biographies
Nils B. Lahr is a mathematics major at Lafayette College. He is interested in computer
programming, computer graphics and data base design. He writes seismological software for the
IASPEI Software Company in Menlo Park CA. He plans to attend graduate school in mathematics
and computer science.

Clifford A. Reiter is an associate professor of mathematics at Lafayette College. He received his
PhD in mathematics from Pennsylvania State University in 1984. He is interested in the use of
computers for insight into mathematical problems with special interest in number theory, numerical
analysis and visualization. He is coauthor of the text APL with a Mathematical Accent.

Figure 1: Newton's method on z³ −1.

Figure 2: Newton's method on .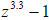

Figure 3: Newton's method on .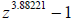

Figure 4: Newton's method on .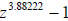

Figure 5: Newton's method on z⁴ −1 .

Figure 6: Newton's method on .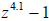

Figure 7: Newton's method on .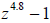

Figure 8: Newton's method on z⁵ −1.

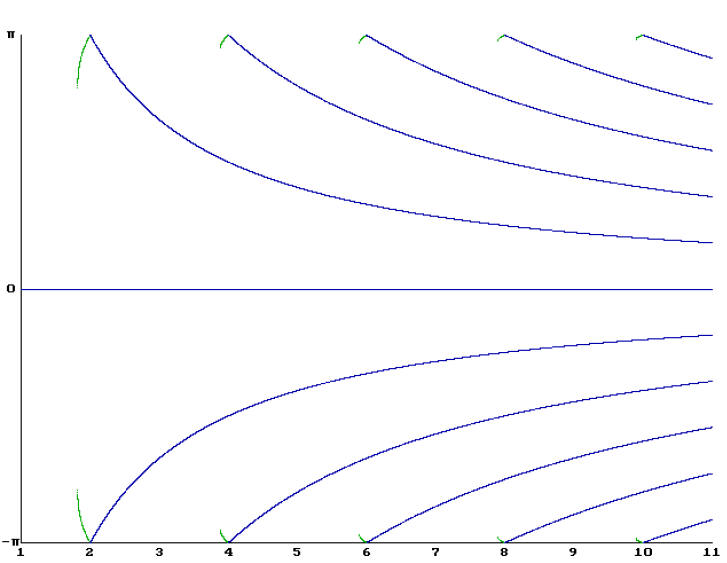
Figure 9: Angle of long term behavior of Newton's method on zα −1 for 1 ≤α ≤ 11.