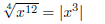TOPICS IN ALGEBRA AND TRIGONOMETRY - Exponents

XXX. Exponents
The simplest exponents are those that are positive integers .

Definition: Let n be a positive integer. Then

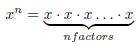
THE TWO MOST IMPORTANT PROPERTIES:

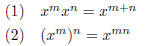
Property (1) says that when you multiply, you add exponents .
Property (2) says that when you raise to powers , you multiply exponenst.
It is essential to completely understand these properties since much of what we do with more complicated
exponents depend on these two properties. In fact, however we define other types of exponents, we want these
two properties to be satisfied. Otherwise, all computations would have to depend on the type of exponents
we are using.

Exercises:
1. Verify property (1).
2. Verify property (2).

Another two properties of exponents are also very important:

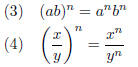
Exercises:
3. Verify property (3).
4. Verify property (4).

Exponents that are not positive integers are much more difficult to understand. For instance, nothing
about the definition for xⁿ where n is a positive integer would tell you what x⁰ should mean. In fact, if you
were to ask your ten year old little sister what you get when you take x times itself zero times,
the response would probably be “Zero”.
However, if property (1) is to be satisfied, we would have the following:

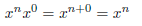
The only way this can happen is if we have the following:

Definition: x⁰ = 1

Now what should be done about an exponent that is a negative integer ? Again, the idea that an
exponent simply means to multiply something by itself a certain number of times would not apply in this
case. What would it mean to multiply x by itself a minus five times ?
We have to go back to property (1) again to see the following would have to work:

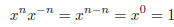
This leads to the following:
Definition:

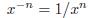
Exercise:

5. Verify the following property:

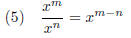
6. Show that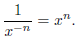

Now we have definitions of exponents which are integers, whether they be positive, negative or zero .
What do we do with rational exponents ?
We now rely on property (2) to see the following would have to be true:

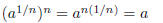
We now recall that 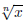represents the number that , when multiplied by itself n times, equals x.
So we have the following:

Definition: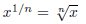

Now we apply property (2) again to see the following:

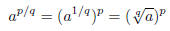
and

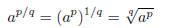
This leads to our definition that works for all rational exponents:

Definition:

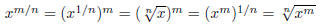
Example 1:

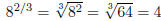
or, more simply:

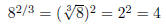
Example 2:

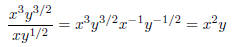
Example 3:

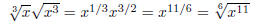
Example 4:

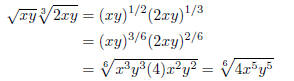
Exercises:

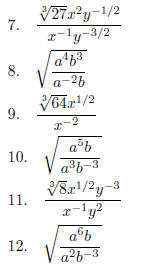
Great care must be taken in working with exponents and radicals . For instance, the following statement
is true:

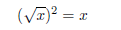
However,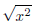is not always equal to x

Example 5:

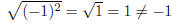
This complication occurs becaue 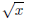represents the principal square root of x , so that we have, for
instance:

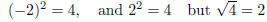
In fact, we can make the following definition of absolute value (not really the best but it is correct):

Definition :

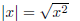
Such complications can occur whenever x can be negative.
Exercises:

13. Show that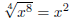

14. Show that