2.3 All the reals from the positive reals
This is more like the passage from the natural numbers to the positive
rationals.
There we were closing up under the operation of division , here we
are closing up under the operation of subtraction. There we used a familiar
simplification to make sure that only one quotient was used to represent each
positive rational , here we use a simplification which is no more complicated
but will not be familiar. Each real number can be expressed in the form
r - s where r and s are positive reals in just one way - if we require that
min(r, s) = 1.
So we define a real number as an ordered pair (r, s) where r and s are
positive real numbers and min(r, s) = 1.
The positive real r will correspond to the general real (r + 1, 1), the
negative real -r will be represented as (1, r + 1), (1, 1) represents 0 (which
now appears for the first time as a first-class citizen of the world of numbers).
We define simp(a, b) as (a+1-min(a, b), b+1-min(a, b)): notice that these
subtractions can be carried out entirely in the positive reals, and that for any
a and b, simp(a, b) will be the real number (according to our definition) which
we expect to represent a - b.
We define (r, s) + (t, u) as simp(r + t, s + u) and (r,
s)(t, u) as simp (rt +
su, ru+st). We define (r, s) ≤ (t, u) as r+u ≤ s+t. Everything here makes
perfect sense if one interprets (r, s) as r - s (that's the whole point). We
leave to the reader the project of showing that all the axioms of sections 3
and 4 hold for the resulting system of real numbers.
3 We make everything go away?
We have explained the entire system of real numbers in terms of the natural
numbers, the notion of ordered pair, and the notion of set.
In this section, we show how to explain the pairs and the natural numbers
as sets, and we give the basic axioms of set theory which are required to
make everything work. In modern mathematics, everything is reduced to the
theory of sets!
We give a first axiom: sets with the same elements are equal.
You probably recall the notation {a, b} for the set whose only elements
are a and b, and {a} for the set whose only element is a.
We define the ordered pair (a, b) as {{a} , {a, b} }. There is a gap here:
one needs to prove that if (a, b) = (c, d), then a = c and b = d. This is a
little involved, but can be proved just from the definitions of the sets and
the axiom given above.
To make sure that we can always build ordered pairs, we introduce another
axiom: for any objects a and b, there is a set {a, b} which has a and
b as its only elements. If a = b, we get the set {a} (so we do not need a
separate axiom for this case).
We introduce another axiom: there is a set Ø, with no elements (it is
straightforward to prove that there can be only one such set).
We introduce a further axiom. For any sets A and B, there is a set A∪B
such that for all x, x ∈ A ∪ B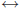 
x ∈ A
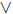x ∈ B. This is the union of A and
B.
We define 0 as Ø, 1 as 0∪{0} = {0}, 2 as 1∪{1} = {0,1}, 3 as 2∪{2} =
{0,1,2}, and so forth.
The "and so forth" should make you suspicious (it is a verbal ellipsis!)
To explain it we introduce a definition and an axiom. We say that a set
I is inductive if it contains {Ø} as an element and contains x ∪ {x} as an
element for each x ∈ I. Notice that Ø is our 1 and for each of our natural
numbers x we have x+1 = x ∪ {x}. The axiom asserts that there is a set N
which has as its elements exactly those sets n which
belong to all inductive
sets: of course we call the elements of N natural numbers.
Notice that 1 belongs to any inductive set, and so do 2,3, and so forth.
Of course we could easily have included 0.
Here is a gap: it can be proved that the axioms N1-5 are true if we take 1
to be the singleton of the empty set, define n+1 as n∪{n}, and take the set
of natural numbers to be defined as our N. (The power set and separation
axioms below are actually needed for this development: defining addition
and multiplication is a bit tricky).
To construct our number systems we need two more axioms, both of which
have to do with subsets. Recall that for sets A and B, we say that A is a
subset of B (A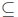 
B) if and only if all elements of A also belong to B.
Power set axiom: for any set A, there is a set P(A) whose elements are
exactly the subsets of A.
Separation axiom: for any set A and property P (x) (this is a sentence
about an object x) there is a set {x ∈ A l P(x)} whose elements are exactly
the elements x of A such that P(x) is true.
Theorem ( cartesian products ): for any sets A and B, the set A × B of
all ordered pairs (a, b) with a ∈ A and b ∈ B exists (hint: it is a subset
of P (P(A ∪ B)): to see this you have to look at the internal details of the
definition of the ordered pair - for the last time!)
Now we can see how the whole construction is done. N is the system of
natural numbers. The system of positive rationals is a subset of N × N which
can be picked out using the separation axiom. The system
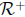of positive real
numbers is a subset of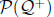 
(it is a set of sets of positive rationals) which
can be picked out using separation. The system R of all reals is a subset
of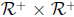 
which can be picked out using separation. The operations on
the various systems of numbers can also be constructed using the basic set
theory axioms.
The set of axioms I have given is not quite the usual one. The axiom
providing A ∪ B is enough for our purposes, but the usual union axiom
asserts the existence of ∪A, the set of all elements of elements of A, for any
set A: A∪B = ∪{A,B} is provided by this axiom. There are a couple more
axioms which usually appear but which are not needed for this construction.
But the exact system of axioms I have given is adequate for the construction
of almost all of mathematics, including all of mathematics which has
any significant application in the sciences. Isn't that interesting?
A final observation: what about the "geometric intuition" I keep men-
tioning? Notice that we can "construct" the Euclidean plane as R ×R, the
set of ordered pairs of real numbers, and similarly for Euclidean three-space
- and just as easily for higher dimensional spaces... What happened?
