MATH 4011 Fall 2009 Some thoughts about proofwriting
Math 3000 is a prerequisite for this course , so you should
already have some exposure to proofs. However,
its not uncommon for students to freak out about trying to prove stuff, because
it seems so different from
the kind of math you may be used to doing. However, the sorts of problems you’ll
do in this course are more
realisitic in the sense that this sort of mathematics is much closer to what
professional mathematicians
actually do (as opposed to balancing checkbooks or multiplying 5 digit numbers
in our heads , contrary to
popular opinion)
When I was an undergraduate, my first exposure to real
analysis was called ‘Math 424’ at the University
of Washington. I had just transferred there, and there was no “proofwriting”
prerequisite. The book we
used was (is) called Principles of Mathematical Analysis, by Walter Rudin. It’s
a hard book. I had an
indifferent teacher. I felt like I had no idea what I was doing and didn’t learn
much. Some of you might
feel the same way in this course at times , and I’ll do my best to help you get
through it, short of “just
giving you the answers” (that would be the biggest crime of all; you’re not
getting out of here without
showing me that you can write a cogent analysis proof). I’ll share here a few
suggestions, based on my
experiences. I’ve been through what you’re about to go through, and it can be
frustrating. It’s up to you
to take or leave this advice; but if I had it to do over again, I like to think
that taking some heed of these
thoughts would be beneficial.
1. DON’T JUMP RIGHT IN. I think the biggest mistake that I
made was trying to prove a claim
before I understood exactly what I needed to do. Before you start trying to
solve a problem ,
make absolutely sure that you have a solid understanding of what’s being asked.
Spend
some time figuring out your starting point and your destination before you try
to get there. In the
long run, this approach will save you time.
(a) Make sure you know the definitions of all the relevant
terms. Write them all down, over and
over if necessary.
(b) Clearly identify the hypotheses in the problem–this is
important because hypotheses are the
things you get to assume are true.
(c) Make absolutely certain that you don’t assume anything
other than the hypotheses in the
problem. A common pitfall is “assuming what you’re trying to prove.” You’ll get
zero points
for this.
2. Make friends with notation. It’s important to be able
to interpret mathematical notation correctly,
and to be able to use it correctly in your writing. Think of it like punctuation
and grammar, only
more important. If your proofs don’t utilize notation correctly, then they lose
their meaning. If you
know how to do a problem correctly, make sure you can write it down correctly.
Cogent written
communication is a big part of the course.
3. The problems you submit should NOT be first drafts. It
usually takes many attempts, false starts,
and do-overs to get a problem right. Plan on writing several drafts (on scratch
paper) of your work.
The write ups that you submit will (and should) be the result of several
attempts.
4. When you get stuck, try thinking about different
approaches. Sometimes, a direct proof is easiest.
Other times, contrapositive or contradiction are easier. There’s no magic bullet
here; it just takes
practice.
Here are a couple of simple examples that demonstrate
my thought process (I’m not writing down
rigorous proofs here though):
1. Prove that the sum of two rational numbers is rational.
Before jumping right in, let’s write this statement
mathematically, (using proper notation!):
If x, y ∈ Q, then x + y 2∈
Q.
Notice that we now have an “if...then” statement, which
helps to clarify our starting and ending
points. From the get-go, we get to assume that each of x and y is a rational
number. What does
this mean? Recall that a number is rational if it can be expressed as the
quotient of two integers
(provided the denominator isn ’t zero). So, we want to show that if x and y can
each be expressed
as a quotient of integers, then their sum is also a quotient of integers. Now
let’s be a little more
formal:
Suppose x = a/b, and y = c/d, where a, b, c, d ∈
Z and b, d ≠ 0. Now,
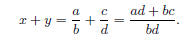
Since a, b, c and d are integers, ad + bc and bd are also integers. Since b ≠ 0
and d ≠ 0, bd ≠ 0.
Therefore, x + y is a quotient of integers, hence it’s rational.
2. Prove that the product of a rational number and an
irrational number is irrational.
This one is a little harder, and it might be tempting to
resort to an argument along the lines of
“even though one of the numbers has the form a/b, the other one doesn’t, so it’s
impossible”, or
“let x ∈ Q and y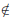 
Q. The decimal expansion of x either terminates or repeats periodically, but the
decimal expansion of y never stops and never repeats. Therefore, the decimal
expansion of xy never
stops and never repeats, so xy is irrational.” This proves nothing, so let’s try
to be more careful.
Start by writing the statement in concise mathematical language:
• If x ∈ Q and y
Q, then xy
Q.
After casting around a bit for a direct proof, you might
get stuck (or maybe not; a direct proof may
be possible, even easy...I just don’t see it right away). So try a different
tactic. The “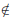
” in the
conclusion “xy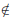 
Q” suggests that we try the
contrapositive: (Recall that the contrapositive of the
statement “if A, then B” is “if not B, then not A.” So:
• If xy ∈ Q, then either x and y
are both rational, or x and y are both irrational (the negation
of “one number is rational and another is irrational” is “either both numbers
are rational, or
both numbers are irrational; there is nothing special about the labels x and y).
OK. So suppose that xy = a/b, where a, b ∈
Z. Now, if x ∈ Q, then x = c/d for some integers c and
d, so
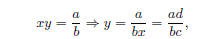
thus y ∈ Q, because ad and bc are both integers. Now,
if you think about it for a second, we’re
done. Why? Let’s examine the remaining possibilities. If x is irrational, then y
can’t possibly be
rational, because if it was, x would have to be rational also, by our previous
argument. So, if x is
irrational, then y must necessarily be irrational as well.
Finally, one comment about the use of examples and
counterexamples. Counterexamples are great
for proving that something isn’t true, but trying to prove a general statement
is true by giving a
specific example isn’t a good idea. For instance, the following is totally
bogus:
Prove that the sum of two rational numbers is rational.
proof: Let x = 1/2 and y = 1/3. Then
x + y = 5/6 which is rational, so x + y is rational. This should make you
cringe.
However, if it is claim is made about a collection of
objects, it must be true for all of them. So if
you can produce a single counterexample, you know the claim must be false. For
instance, we can
show that the sum of two irrational numbers is not necessarily irrational by
actually coming up with
two irrational numbers whose sum is rational. I thought of these: let x =
0.121221222122221 . . .,
and let y = 0.545445444544445 . . .. Both x and y are irrational, since their
decimal expansions are
non- terminating and non -repeating. But x + y = 0.66666666 . . . = 2/3, which is
rational.
