Solving Uniform Motion Problems using Systems of Equations

The distance d traveled by an object moving in a straight line at constant rate r for time t is
given by



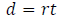
provided that the unit of the time component of r is the same as the unit for t.

Each of the problems below can be solved by using a system of two linear equations in two
variables. After defining two variables , write one equation involving rate and another equation
involving distance. Solve the system of the two equations then use the solution to answer the
question.

Example: Two cars, one traveling 12 mph faster than the other, start at the same time from the
same point and travel in opposite directions. In 4 h, they are 384 mi apart. Find the rate of
each car.

Step 1: Use two variables to define two unknown quantities.

Let x represent the speed of the slower car.

Let y represent the speed of the faster car.

Step 2: Write an equation involving rate.



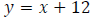
Step 3: Write an equation involving distance.

The distance between them, 384 mi, can be expressed as the sum of the distances each
car has traveled. Each car’s distance can be expressed as the product of the time it has
traveled and its rate. Thus, we have the equation



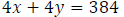
Step 4: Solve the system consisting of the equations from Steps 2 & 3.

Solution: (42, 54)

Step 5: Use the solution of the system to answer the question.

The cars are traveling at 42 mph and 54 mph.

Example: A car and a bus set out at 3 p.m. from the same point headed in the same direction.
The average speed of the car is twice the average speed of the bus. In 2 h, the car is 68 mi
ahead of the bus. Find the rate of the car.

Step 1: Use two variables to define two unknown quantities.

Let x represent the speed of the car.

Let y represent the speed of the bus.

Step 2: Write an equation involving rate.

Since the car’s speed, x, is twice the speed of the bus, y, we have the equation



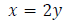
Step 3: Write an equation involving distance.

After they both travel for two hours , the distance traveled by the car is 68 mi more than
the distance traveled by the bus.



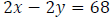
Step 4: Solve the system consisting of the equations from Steps 2 & 3.

Solution: (68, 34)

Step 5: Use the solution of the system to answer the question.

The car is traveling at 68 mph.

Try this one in class: Two cyclists start from the same point and ride in opposite directions.
One cyclist rides twice as fast as the other. In 3 h, they are 81 mi apart. Find the rate of each
cyclist.

Homework: Use a system of equations to determine the answer to each question.

1. Two planes start from the same point and fly in opposite directions. The first plane is flying 25
mph slower than the second plane. In 2 h, the planes are 470 mi apart. Find the rate of each
plane.

2. A passenger train leaves a train depot 2 h after a freight train leaves the same depot. The
freight train is traveling 20 mph slower than the passenger train. Find the rate of each train if
the passenger train overtakes the freight train in 3 h.

3. A bus traveled on a straight road for 2 h at an average speed that was 20 mph faster than its
average speed on a winding road. The time spent on the winding road was 3 h. Find the
average speed on the winding road if the total trip was 210 mi.

Each of the problems below can be solved by using a system of two linear equations in two
variables. After defining two variables , write one equation involving the time spent in motion
and another equation involving distance. Solve the system of the two equations then use the
solution to answer the question.

Example: A pilot flew to Newark and back. The average speed going was 320 mph. The
average speed returning was 480 mph. Find the distance to Newark if the total flying time was
5h.

Step 1: Use two variables to define two unknown quantities.

Let x represent the time it took the plane to go to Newark.

Let y represent the time it took to return back from Newark.

Step 2: Write an equation involving travel time.



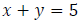
Step 3: Write an equation involving distance.

The distance to and from Newark is the same. Thus, we have the equation



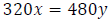
Step 4: Solve the system consisting of the equations from Steps 2 & 3.

Solution: (3, 2)

Step 5: Use the solution of the system to answer the question.

It took 3 h to fly to Newark. Since the plane was traveling to Newark at 320 mph, the
distance to Newark is 960 mi. (To check, make sure the return distance, 2 h × 480 mph,
is also 960 mi.)

Example: A 555‐mi, 5‐hour plane trip was flown at two speeds. For the first part of the trip,
the average speed was 105 mph. For the remainder of the trip, the average speed was 115
mph. How long did the plane fly at each speed?

Step 1: Use two variables to define two unknown quantities.

Let x represent the time traveled at 105 mph.

Let y represent the time traveled at 115 mph.

Step 2: Write an equation involving travel time.



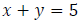
Step 3: Write an equation involving distance.



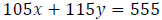
Step 4: Solve the system consisting of the equations from Steps 2 & 3.

Solution: (2, 3)

Step 5: Use the solution of the system to answer the question.

The plane flew for 2 hr at 105 mph and 3 hr at 115 mph.

Try this one in class: A jogger starts from one end of a 15‐mi nature trail at 8:00 a.m. One hour
later, a cyclist starts from the other end of the trail and rides toward the jogger. If the rate of
the jogger is 6 mph and the rate of the cyclist is 9 mph, at what time will the two meet?

Homework: Use a system of equations to determine the answer to each question.

4. One speed skater starts across a frozen lake at an average speed of 8 meters per second. Ten
seconds later, a second speed skater starts from the same point and skates in the same
direction at an average speed of 10 meters per second. How many seconds after the second
skater starts will the second skater overtake the first skater?

5. An executive drove from home at an average speed of 30 mph to an airport where a helicopter
was waiting. The executive boarded the helicopter and flew to the corporate offices at an
average speed of 60 mph. The entire distance was 150 mi. The entire trip took 3 h. Find the
distance from the airport to the corporate offices.

6. A car traveling at 48 mph overtakes a cyclist who, riding at 12 mph, had a 3 hour head start.
How far from the starting point does the car overtake the cyclist?

Rate‐of‐Wind or Water Problems

Suppose that a plane flies in calm air at x mph. Suppose also that the wind is blowing at a rate
of y mph. If the plane is flying in the direction of the wind, it actually travels, with respect to
the ground, faster than it normally would in calm air. In fact, the plane’s rate with the tailwind
is actually (x + y) mph. On the other hand, if the plane is flying directly into the wind, it is
slowed down to a rate of (x – y) mph

Each of the problems below can be solved by using a system of two linear equations in two
variables. Let x be the rate of the plane (or boat, or other object) under calm conditions. Let y
be the rate of the wind (or current, or other force).

The rate of the plane when traveling with the wind is x + y, and

the rate it travels when flying against the wind is x – y.

For each problem, write an equation about distance when the plane flies with the wind, and
write another equation about distance when the plane is flying into the wind. Solve the system
of the two equations then use the solution to answer the question.

Example: Traveling with the current, a boat traveled 22 mi in 2 h. Traveling against the
current, the boat traveled 10 mi in 2 hr. Find the rate of the boat in calm water and the rate of
the current.

Step 1: Use two variables to define two unknown quantities.

Let x represent the rate of the boat in calm water.

Let y represent the rate of the current.

Step 2: Write an equation involving distance when traveling with the current.



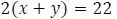
Step 3: Write an equation involving distance when traveling against the current.



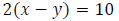
Step 4: Solve the system consisting of the equations from Steps 2 & 3.

Solution: (8, 3)

Step 5: Use the solution of the system to answer the question.

The boat travels in calm water at 8 mph and the current is moving at 3 mph.

Example: A plane flying with the jet stream flew from Los Angeles to Chicago, a distance of
2250 mi, in 5 h. Flying against the jet stream, the plane could fly only 1750 mi in the same
amount of time. Find the rate of the plane in calm air and the rate of the wind.

Step 1: Use two variables to define two unknown quantities.

Let x represent the rate of the plane in calm air.

Let y represent the rate of the wind.

Step 2: Write an equation involving distance when traveling with the wind.



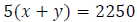
Step 3: Write an equation involving distance when traveling against the wind.



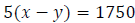
Step 4: Solve the system consisting of the equations from Steps 2 & 3.

Solution: (400, 50)

Step 5: Use the solution of the system to answer the question.

The plane travels in calm air at 400 mph and the wind is blowing at 50 mph.

Try this one in class: With the wind, a quarterback passes a football 140 ft in 2 s. Against the
wind, the same pass would have traveled 80 ft in 2 s. Find the rate of the pass and the rate of
the wind.

Homework: Use a system of equations to determine the answer to each question.

7. A whale swimming against an ocean current traveled 60 mi in 2 h. Swimming in the
opposite direction, with the current, the whale was able to travel the same distance in
1.5 h. Find the speed of the whale in calm water and the rate of the ocean current.

8. A motorboat traveling with the current went 35 mi in 3.5 h. Traveling against the
current, the boat went 12 mi in 3 h. Find the rate of the boat in calm water and the rate
of the current.

9. A private Learjet 31A transporting passengers was flying with a tailwind and traveled
1120 mi in 2 h. Flying against the wind on the return trip, the jet was able to travel only
980 mi in 2 h. Find the speed of the jet in calm air and the rate of the wind.

10. A seaplane flying with the wind flew from an ocean port to a lake, a distance of 240 mi
in 2 h. Flying against the wind, it made the trip from the lake to the ocean port in 3 h.
Find the rate of the plane in calm air and the rate of the wind.