1 Review of the last lecture
Success in algebra depends on having a good understanding of the concepts as
well as on being able to perform the various computations. Like polynomials ,
rational expressions appear frequently in Algebra II and higher mathemat-
ics. Thus, we must understand how to perform basic operations with rational
expressions and how to solve rational equations .
Compare arithmetic - rational numbers with algebra - rational expressions.
Since rational expressions are just fractions with variables in the numerator
and/or denominator, we started by reviewing operations with fractions that do
not contain variables. Then we moved on to performing the same operations on
rational expressions.
1.1 Mulitiplication
When working with multiplication problems , you should begin by factoring any
terms that can be factored . Once you have the problem in factored form , divide
out any common factors and simplify the expression .
1.2 Remark: The Domain of Rational Expressions
When talking about rational expressions, you should always keep in your mind
that the denominator CANNOT be zero. This is so important that I want to
emphasize it as much as I can.
We have a restriction on the values we can plug in to any rational expres-
sion. Specifically, we can not have a denominator of zero. This means that the
expression is undefined for whatever Q values make the denominator equal to
zero. In general, the domain of an algebraic expression is the set of all
numbers
for which the expression is defined. Since rational expressions are undefined
when the denominator is zero, the domain of a rational expression is the set of
all numbers such that the denominator is not zero.
2 Dividing Rational Expressions
Note: In this lesson, students will learn to divide rational expressions. The
techniques are completely analogous to dividing rational numbers (fractions).
Point out, and continue to stress this analogy throughout the entire lesson.
Division problems will follow the same process as multiplication only with
an additional step at the beginning. The first step you have to do is to find the
reciprocal (or flip) the second fraction and change the problem to a multipli-
cation problem. Once it is in the form of a multiplication problem, follow the
same steps as in the previous examples . In one sentence, division can be done
just by multiply by the reciprocal of the divisor .
Definition We call the numbers c/d and d/c reciprocals or multiplicative
inverses
of each other because their product is 1.
Thus we can describe division by saying to divide by a fraction, multiply
by its reciprocal.
2.1 Philosophy
The fundamental guideline in learning mathematics is to change/reduce the new
mathematical problem into those you have learned before.
2.2 Dividing Rational Numbers
Begin by reminding students that to divide rational numbers, use the "invert
and multiply" rule. That is, invert the divisor (take the reciprocal), and then
multiply by the numerator.
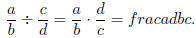
Then simplify by dividing by the common factors of the numerator and the
denominator .
Do the following example on the chalkboard.
Example: Find
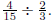
Solution: Take the reciprocal of the divisor ( 2/3 ) and multiply.
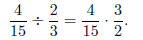
Before multiplying, look for common factors.
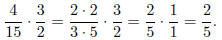
So we conclude that
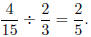
2.3 Dividing Rational Expressions
Dividing rational expressions is done the same way. Take the reciprocal of
(invert) the divisor and then multiply by the numerator. Then simplify by
dividing the common factors of the numerator and the denominator. Do the
following example on the chalkboard.
Example: Find
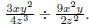
Solution: Take the reciprocal of the divisor and multiply.
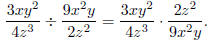
Before multiplying, look for common factors.
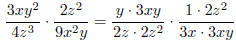 (Cancel
the common factors)
(Cancel
the common factors)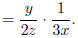
So we conclude that
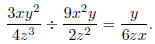
There are some problems involving division of rational expressions that re-
quire factoring of polynomials in order to find common factors of the numerators
and the denominators.
Example: Find
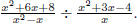
Solution: Take the reciprocal of the divisor and multiply.
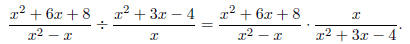
Before multiplying, factor the quadratic terms in these quadratic expressions
in
order to find common factors.
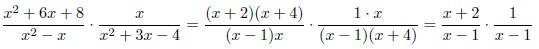
So, we conclude that
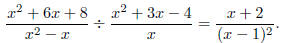
Example: Divide and simplify
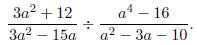
Solution:
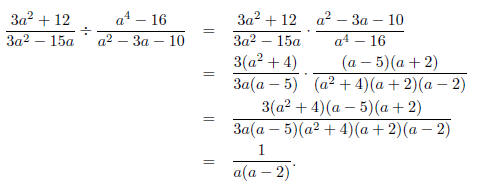
Example: Divide and simplify
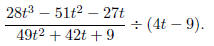
Solution:
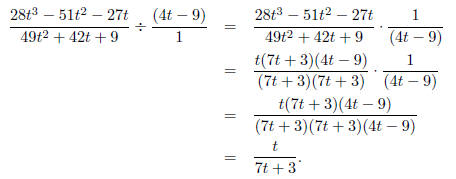
Example: Divide and simplify
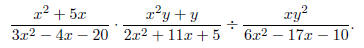
Solution:
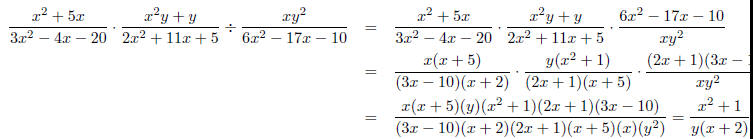
Remark This technique is very important because it reinforces prior
techniques
like multiplying rational expressions, factoring quadratic expressions, and
divid-
ing rational numbers. Give your students many practice problems.
3 Summary
Another strategy for studying mathematics is to do the summary job and to
compare similar concepts or operations after a period of study.
• Rational Expressions:
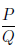
where P and Q are polynomials, and Q ≠ 0.
• To Simplify Rational Expressions:
- Factor both the numerator and denominator
- Divide both the numerator and the denominator by any common
factors.
• To Multiply Rational Expressions:
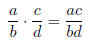
where b ≠ 0 and d ≠ 0.
- Factor all numerators and denominators
- Divide out any common factors
- Multiply using the above rule
- Simplify
• To Divide Rational Expressions:
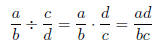
where b ≠ 0, c ≠ 0, and d
≠ 0.
- Invert the divisor
- Follow steps to multiply rational expressions



