A. Rational Numbers
1. Before we discuss irrational numbers, it would probably
be a good idea to define rational
numbers.
| Definition: Rational Number
A rational number is a number that can be written as
a ratio (i.e. fraction) a/b,
where a and b are integers (and b ≠ 0 ). |
2. Examples of rational numbers:
a) 2/3
b)
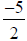
c)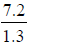
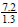is a rational number because it is equivalent to
.
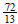d) 6
6 is a rational number because it is equivalent to 6/1 .
e) -4
-4
is a rational number because it is equivalent to
.
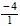f) 0.2
0.2
is a rational number because it is equivalent to
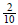(or 1/5 ).
g)
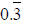
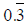is a rational number because it is equivalent to 1/3 .
Note: Any terminating decimal (such as 0.2, 0.75, 0.3157)
is a rational number. Any
repeating decimal (such as
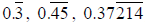) is a rational number. (There are
mathematical ways of converting repeating decimals to fractions which will not
be
covered in this workshop.)
Can you think of any numbers that are not rational
numbers?...
B. Irrational Numbers
1. The technical definition of an irrational number is
that it is a “ real number which is not a
rational number.” So what does an irrational number look like ?
| An irrational number is a nonterminating,
nonrepeating decimal. |
2. A few examples of irrational numbers are π ,
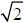, and
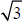. (In fact, the square root of
any prime number is irrational. Many other square roots are irrational as well.)
The values of π ,
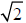, and
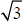are shown below to 50 decimal places . (Notice the
nonrepeating nature of the numbers.)
π ≈
3.14159265358979323846264338327950288419716939937510...
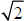≈1.41421356237309504880168872420969807856967187537694...
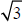≈1.73205080756887729352744634150587236694280525381038...
We will now focus more on how to calculate and simplify
square roots.
C. Evaluating Rational Square Roots
1. Recall how to find square roots:
a)
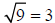, since 3•3 = 9
b)
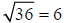, since 6•6 = 36
c)
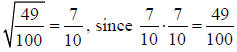
Note: If we solve an equation such as x2=25 , we take the
square root of both sides and obtain a solution
of x=± 5 . However, the “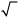
” symbol denotes the principle square root and represents only the
positive square root. Therefore we say, for example, that
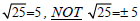
2. Evaluate the following without a calculator. Give exact
answers:
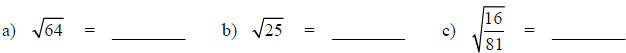
D. Approximating Square Roots
1. We will first use the graph of
to approximate square roots. To graph
, let
us first make a chart with a few x and y values:
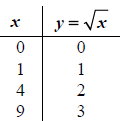
If we plot the above points and then draw a smooth curve
through them, we obtain the
following graph of
:
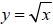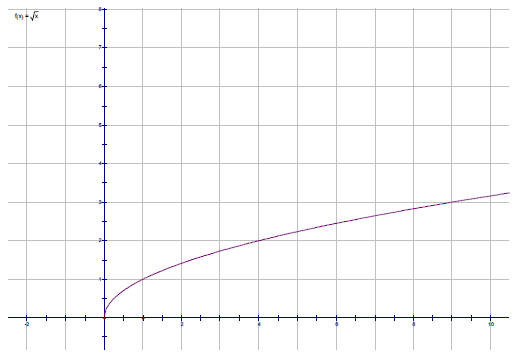
By looking at the graph, we can get a general idea of the
value of some irrational square
roots:
a) Use the graph to estimate the value of
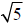to the nearest tenth. __________
b) Use the graph to estimate the value of
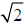to the nearest tenth. __________
c) Use the graph to estimate the value of
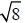to the nearest tenth. __________
d) Compare the values you obtained for
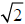and
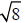. Do you notice any relationship
between them? ______________________________________.
e) Fold the graph so that the point
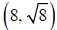is on top of the point (8, 0). After
unfolding your paper, look to see where the crease hits the graph. Does this
verify
the relationship that you found in part (d)? _____________________________
2. Mental Estimation of Square Roots
Suppose that we want to estimate the value of
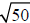. It may not be reasonable to extend
the above graph to an x value of 50 so approximate this square root. To estimate
square
roots mentally, it is useful to refer to a list of perfect squares :
12 =1
22 = 4
32 = 9
42 =16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 =100
 |
 |
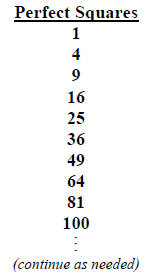If we want to estimate the value of
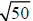, for example, we can use the perfect squares list
in this way: The number 50 is between the perfect squares 49 and 64. Therefore,
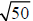is
between
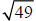and
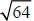. So
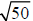has a value between 7 and 8.
Examples: Estimate the following square roots, using the
method from above .
a)
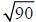
The number 90 is between the perfect squares ______ and ______. Therefore,
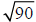is
between
and
. So
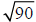has a value between ______ and ______.
b)
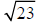
The number 23 is between the perfect squares ______ and ______. Therefore,
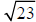is
between
and
. So
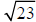has a value between ______ and ______.
