Day 4
Lesson Plan:
Objectives:
1. Students will be able to use quadratic equations to solve problems about
paths of
projectiles.
Standards:
• NCTM Standards covered: Algebra , Representation
• NYS Standards covered: 7A, 7C, 7D
Materials:
• Blank sheet of overhead transparency
• Overhead
Opening Activity:
As students enter the room they will be divided into their groups to discuss
their projects.
The students will be given the first 10 minutes of class to discuss project
progress and the
teacher will circulate about the room to answer questions.
Developmental Activity:
The students will remain in their groups to discuss the following question. List
as many
objects as you can that are either in the shape of a parabola or travel in the
path of a
parabola. For example the water that comes out of the drinking fountain. The
groups
will have time to discuss and then the teacher will pass around the blank sheet
of
transparency and have the groups add to the list as it gets to them. We will
then discuss
as a class.
Ticket Out:
Students will have the last 5 minutes of class to respond to the following
question, also to
address any concerns they had with the lesson.
Are there any items on the list that need to be further discussed to prove to
you that their
paths a parabolas?
Homework:
Read pgs. 567 – 569, complete pg. 569 # 12 –15.
Teacher’s Notes:
Developmental Activity:
This activity is designed to make the students relate parabolas to their
everyday life. It
will also help them to better understand the reading and the homework problems.
Solutions to Homework :
12. 45 meters
13. 25 meters
14. after 2 and 4 seconds
15. 35 meters
Day 5
Lesson Plan:
Objectives:
1. Students will be able to solve quadratic equations using the quadratic
formula.
2. Students will be able to solve quadratic equations using the PolySmlt App.
Standards:
• NCTM Standards covered: Algebra, Representation
• NYS Standards covered: 2A, 3A, 7A, 7C
Materials:
• Graphing calculators and overhead unit
• Worksheet for students with overhead transparency
Opening Activity:
The students will answer these questions when they enter the room.
Evaluate each expression when a = a, b = -5, and c = 1.
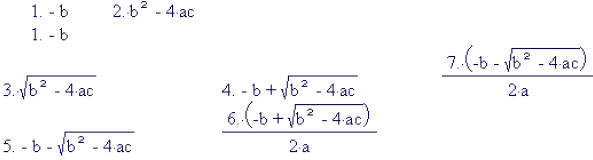
Developmental Activity:
The students will work with a partner to complete the Quadratic Formula
worksheet .
Students will be called to the board to show solutions.
Ticket Out:
Students will have the last 5 minutes of class to respond to the following
question, also to
address any concerns they had with the lesson.
What happens when b2 – 4ac is a negative number?
Homework:
Read pgs. 573 – 576 , complete pg. 577 # 5 – 8, 15.
Teacher’s Notes:
Solutions to Opening Activity:
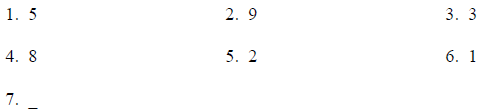
Solutions to Developmental Activity:
1. x = 1.5 or - 2
2. x = -2
3. x = 5 or – 5
4. x = 2 or 5
5. x = - 2/3 or 7/4
6. no real solutions
Solutions to Homework:
| 5a. a = 12, b = 7, c = 1 |
b. x = - _ or x = 1/3 |
| 6a. a = 3, b = 1, c = -2 |
b. x = 2/3 or x = -1 |
| 7a. a = 1, b = 6, c = 9 |
b. x = -3 |
| 8a. a = -1, b = 0, c = 4 |
b. x = -2 or x = 2 |
15a. 2.5 and 5.0
15b.
Solving Quadratics
Name: ____________________
Period: _____
Directions: Solve each of the following quadratic equations using the Quadratic
Formula listed below. Show all work.



Directions: Using the same six equations above check your
answers using the PolySmlt
App on your calculator. Choose Poly Root Finder with degree 2. Remember
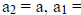
b, and 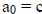 .
.

Unit Test
Graphing and Solving Quadratics
Name: ____________________
Period: _____
Directions: Answer all questions on this test. You may use your graphing
calculator for
any problem on this test. You must show work on the Quadratic Formula questions
but
you may check your answers with the PolySmlt App.
Graph the following equations. Also draw the axis of symmetry.
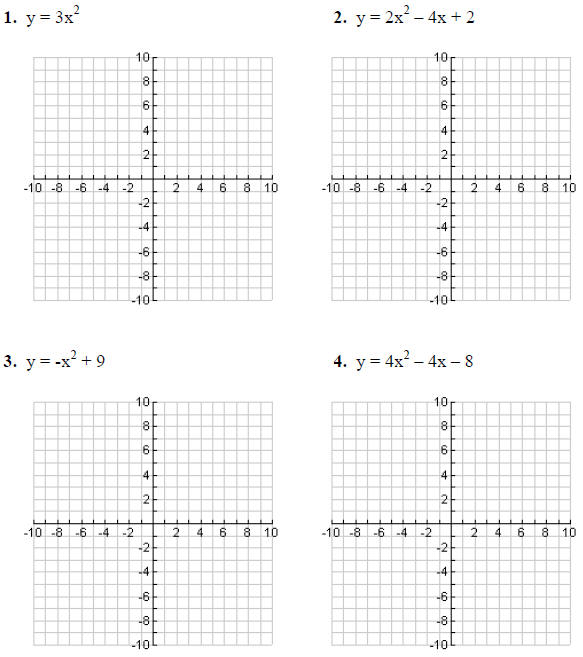
For questions 5 and 6 identify the vertex , the axis of
symmetry, and the y- intercept .
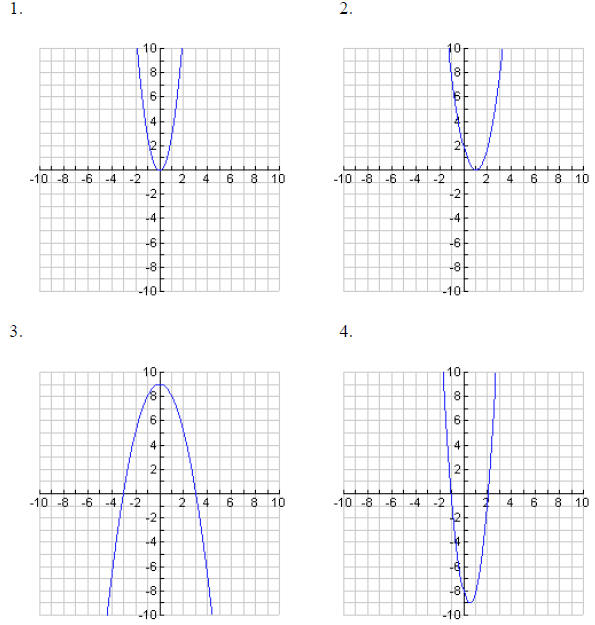
| 5. y = x2 – 25
vertex: (0, -25)
axis of symmetry: x = -25
y-intercept: (0, -25) |
6. y = 2x2 – 4x + 5
vertex: (1, 3)
axis of symmetry: x = 1
y-intercept: (0, 5) |
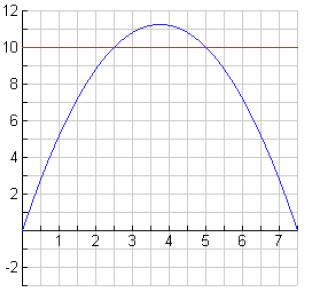
7. One of the first astronauts who traveled to the moon hit a golf ball on the
moon.
Suppose that the height h in meters of a ball t seconds after it is hit is
described by
h = 0.8t2 + 10t.
a. Graph the equation.
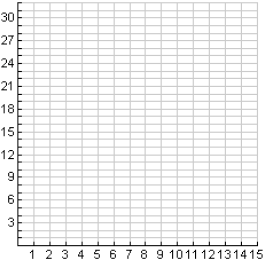
b. Find the times at which the ball is at a height of 20
meters.
Solve for x using the Quadratic Formula. Show all work!
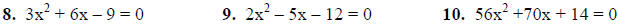
Answer Key to Unit Test
| 5. y = x2 – 25
vertex: (0, -25)
axis of symmetry: x = -25
y-intercept: (0, -25) |
6. y = 2x2 – 4x + 5
vertex: (1, 3)
axis of symmetry: x = 1
y-intercept: (0, 5) |
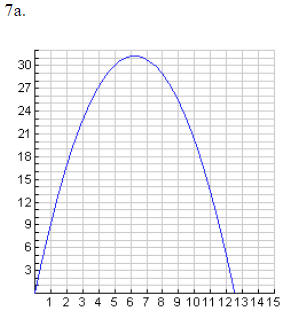
7b. 2.5 and 10 seconds
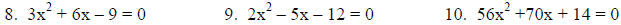 |
| x = 1 or –3 |
x = -3/2 or 4 |
x = -1/4 or –1 |



