Grade 8 Tennessee Middle/Junior High School Mathematics
Contest
16. Hypotheses:
Some gidgets are widgets.
No gadgets are gidgets.
Given the above hypotheses, which is a valid conclusion?
a. Some widgets are not gadgets.
b. No gadgets are widgets.
c. Some gadgets are widgets.
d. All gadgets are widgets.
e. No valid conclusion can be reached from these hypotheses.
17. What is the ratio of the volume of a cube to its surface area if the length
of a side is s?
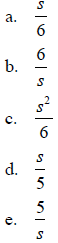
18. A function is defined as f (x) = 3x + 4. The inverse
of a function “undoes” the function.
Which of the following statements is true?
a.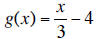 
is the inverse of f(x).
b. There is no function that is the inverse of f(x).
c.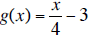 
is the inverse of f(x).
d.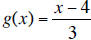 
is the inverse of f(x).
e.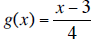 
is the inverse of f(x).
19. The mean high temperature in Nashville for the first twenty-one days of
February was 46
degrees. What must the mean high temperature for the days from February 22 to
February
28 be in order to raise the mean temperature for the entire month to 50 degrees?
a. 54°
b. 56°
c. 58°
d. 60°
e. 62°
20. The length of a rectangle is increased by 20% and its
width is increased by 50%. What is
the percent increase in its area?
a. 10%
b. 30%
c. 70%
d. 80%
e. 100%
21. Pat has a collection of stickers for numbering pages in a scrapbook. Each
sticker has 1 digit
on it (0, 1, 2, 3, 4, 5, 6, 7, 8, or 9). Pat has twenty- two stickers that have
"2" on them. Pat
has plenty of the rest of the digits. If Pat starts at 1, how many pages can he
number?
a. 22
b. 99
c. 112
d. 119
e. 199
22. In my pocket, I have only dimes and quarters. I have
twice as many dimes as quarters and I
have at least one quarter . If the number of dimes and quarters is reversed, by
what percent
will the value of the money in my pocket increase?
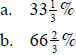
c. 50%
d. 150%
e. 100%
23. In modular arithmetic , the statement 15 ≡ 3 mod 4 means that 15 and 3 both
have the same
remainder when they are divided by 4. These would all be true statements in
modular
arithmetic:
12 ≡ 7 mod 5
7 ≡ 13 mod 2
14 ≡ 42 mod 7
Consider the following statement where, a, b, c, d, and m are whole numbers {0,
1, 2, 3, ...}.
A: If a ≡ b (mod m) and c≡ d (mod m), then (a + b) ≡ (c + d) (mod m)
B: If a ≡ b (mod m) and c≡ d (mod m), then ( a · b) ≡ ( c · d ) (mod m)
C: If a ≡ b (mod m), then ( ac ) ≡ ( bc ) (mod m)
Which of the following is true?
a. Only Statement A is true for all whole numbers a, b, c, d, and m.
b. Only Statement B is true for all whole numbers a, b, c, d, and m.
c. Only Statement C is true for all whole numbers a, b, c, and m.
d. All three statements are true.
e. None of the statements is true for all whole numbers a, b, c, d, and m.
24. Which of the following pairs of algebraic expressions are equivalent ?
a. (x + 2)2 x2 and 2(x + 2) + 2x
b. (x + 3)2 and x2 + 9
c. 2(xy) and 2x · 2y
d.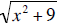 
and x + 3
e. 0x0 and 00
25. A nickel, a dime, and a penny are tossed. What is the probability that they
do not all land
the same way—they are not all either heads nor are they all tails?
a.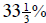 
b. 20%
c. 50%
d. 25%
e. 75%
26. The graph below shows the distribution for 100 rolls
of two dice.
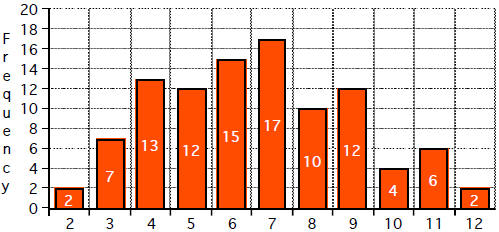
Sum of Two Dice
Which statement is true about the distribution of the sums of the two dice?
a. The standard deviation is 0.
b. The mean is 9.09.
c. The median is 6.
d. The mean is 6.64
e. The median is 6.5
27. When 1093 - 93 is expressed as a single whole number, what is the
sum of its digits?
a. 10
b. 93
c. 819
d. 826
e. 833
28. A calculator displays 5.1698788285E+58 when 2542 is entered.
Which statement is true?
a. The answer displayed is not exact.
b. The answer to 2542 would have 58 zeros at the end, if the
calculator had a big enough
display.
c. The answer to 2542 would have 48 zeros at the end, if the
calculator had a big enough
display.
d. The answer to 2542 would have 47 zeros at the end, if the
calculator had a big enough
display.
e. The answer to 2542 would have 49 zeros at the end, if the
calculator had a big enough
display.
29. A student sketched a graph of a situation as shown
below:
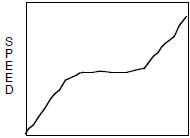
TIME
Which situation would fit the above sketch?
a. A runner ran up a hill at a constant speed. The runner slowed down halfway up
the
hill and then sped back up again.
b. A runner ran down a hill at a constant speed. The runner stopped to drink
some
water. Then the runner started running at a constant speed again.
c. A runner started at the top of a hill. As he ran down, he gained speed. When
he got
to a level part, he maintained his speed at a constant rate. Then the runner
started
speeding up again.
d. A runner started a race at a constant speed. Then the runner gained speed
during the
middle of the race. Finally the runner ended at a constant speed that was faster
than
her beginning speed.
e. A runner started a race running very slowly and gradually accelerated at a
constant
rate throughout the race.
30. A triangle has vertices A (3, 7), B (0, -1), and C (6, 2). The coordinates
of each point are
multiplied by 6 to produce three new points. The new points are the vertices of
a second
triangle. Which statement is true?
a. The new triangle is not necessarily similar to the original triangle.
b. The area of the new triangle is 36 times the area of the original triangle.
c. The perimeter of the new triangle is 36 times the area of the original
triangle.
d. The area of the new triangle is 6 times the area of the original triangle.
e. The new triangle is congruent to the original triangle.
