Fundamental Concepts of Algebra

Notes - Week 3

1. Let p and q be prime numbers. It is known that both roots of

x² + px + q

are integers. Find p and q .

2. Find a quadratic polynomial whose roots are the reciprocals of the roots of

5x² - 7x - 13.

3. Consider the quadratic equation

x² + 4x + 1 = 0.
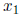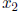Without computing its roots and find

(a)
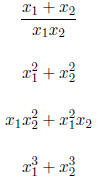(b)
(c)
(d)

4. Derive Vieta's formulas for the cubic polynomial

ax³ + bx² + cx + d.

Solving Inequalities

Let's look at another problem related to finding roots of a quadratic equation.

Example 1. Investigate the signs of the roots of the quadratic equation

(a - 4)x² - 2ax + a + 4 = 0

depending on the value of the parameter a.
First of all we need to understand how many roots that equation has depending
on the value of a. For this we find its discriminant



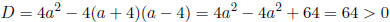
Hence the quadratic equation has two roots for every a. We have to be careful
here. When a = 4 the coefficient of x ² is zero and the equation is not quadratics
anymore. In this case it has just one root x = 1 (check!) When a ≠ 4 using the
quadratic formula we find

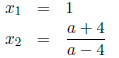
Hence one of the roots is always positive. Let's see when the second root is
positive.

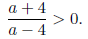
To solve this inequality we use the intervals method which we will discuss in detail
later. We plot a = 4 and a = -4 on the number line with empty dots "o"
(idicating that these points do not satisfy the ineqaulity) and figure out the signs
of (a + 4)/(a - 4) on the obtained intervals.

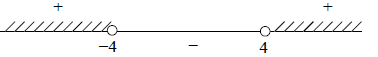
Hence the second root is positive if a ∈ (-∞,-4) ∪ (4,∞). Similarly, the second
root is negative if a ∈ (-4, 4).

We now know what is going on for each value of a except a = -4. In this case
the product of roots is zero and hence one of the roots is zero while the other is
1.Answer:

a ∈ (-∞,-4) ∪ (4,∞) two positive roots

a ∈ (-4, 4) one root is positive, another is negative

a = 4 unique root, positive

a = -4 one root is zero, another is positive

Inequalities occur in numerous other contexts. We now turn to various tech-
niques of solving inequalities. Inequalities in one variable x are of the form

f(x) > g(x), f(x) < g(x), f(x) ≥ g(x), f(x) ≤ g(x):

To solve an inequality means to find its solution set , all the values of the variable
x which satisfy the inequality. Two inequalities are equivalent if they hold for the
same values of x, that is, if their solution sets coincide. In the process of solving
an inequality we are trying to reduce it to a simpler equivalent inequality. Recall
that "" means "equivalent".
Here are three basic rules for handling inequalities. The sign ">" below can be
replaced with "<", "≥ ", or "≤ ".

Rules for Handling Inequalities

• We can add any constant a to both sides of an inequality.

f(x) > g(x) 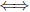f(x) + a > g(x) + a

• We can multiple both sides of an inequality by a positive number a.

if a > 0, f(x) > g(x) 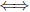af(x) > ag(x)

•If we multiply both sides of an inequality by a negative number a, the in-
equality switches:

if a < 0, f(x) > g(x) 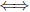af(x) < ag(x)

We will often use these rules to reduce our inequality to the simplest form and
will the use the intervals method to solve the obtained inequality.

Intervals Method

This method is used to solve inequalities of the form

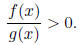
Here the sign ">" could be replaced with "<", " ≥ ", or " ≤ ".
(a) Find the points where f(x) or g(x) are either zero or change sign . If f(x) and
g(x) are polynomials, those points are the roots of f(x) = 0 and g(x) = 0.
Mark those points on the number line with a filled dot " • " if the point satisfies
the inequality and with an empty dot " o " otherwise.

(b) For each of the obtained intervals figure out the sign of f(x)/g(x) and write
that sign next to the interval. Shade the values that satisfy the inequality.

Example 2. Solve the inequality

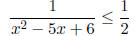
It is tempting to multiply both parts by x² - 5x + 6 here. Notice that if we do
this we have to consider cases when x² - 5x + 6 > 0 and x² - 5x + 6 < 0 so that
we know if the inequality switches sign or not. This is doable, but let's instead
subtract 1/2 from both sides and clear the denominators:

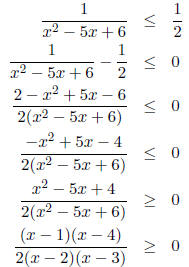
We are now ready to use the intervals method. Notice that the roots of the
numerator x = 1 and x = 4 are marked with filled dots " • " as they satisfy the
inequality.

Answer: (-∞, ∞] ∪ (2, 3) ∪ [4,∞)

Notice how the signs alternate in the picture above. This is always the case if
both f(x) and g(x) in the inequality f(x)/g(x) > 0 are polynomials that do not
contain factors of the form (x-a)²ⁿ (the degree is even). If either in f(x) or g(x)
we have such a factor the sign of f(x)/g(x) does not change as we pass from one
side of x = a to the other.

Example 3. Solve the inequality

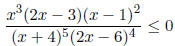
Here is the picture we get.

Notice that the sign does not change at x = 3 and x = 1 as the corresponding
terms 2x - 6 and x - 1 appear in the inequality in even degrees (4 and 2).
Answer: (-∞,-4) ∪ (0, 3/2]

Example 4. Solve the inequality

2x² + 3x + 4 ≥ 0

This quadratic function has negative discriminant and hence has no x- intercepts .
The graph is a parabola that opens upward, hence the function is always positive.
Answer: (-∞,∞)

Example 5. Solve the inequality

3x² - 4x + 2 < 0

This quadratic function has negative discriminant and hence has no x-intercepts. The
graph is a parabola that opens upward, hence the function is never negative.
Answer:

Solve the inequalities.

1.
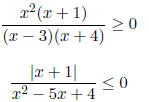2.

3.
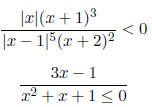4.

Find the domain.

5.
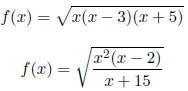6.

Solve the inequalities.

7.
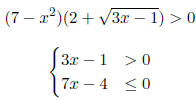8.