Instructions. This take-home exam will be due on
Wednesday, October 8 at 10:20 am. The exam is worth 100 points.
Answer all the questions. You may use your text, notes, and if necessary a
calculus textbook. You MAY NOT consult
with any of your classmates or use any sources other than those enumerated
above. Show all of your work and BE
NEAT. You should have more than sufficient time to prepare a careful , neat exam
to hand in, I will most intolerant of
messy, disorganized work. Be sure to write out and sign the Honor Code on your
exam, an unpledged exam will incur
an automatic 20 pt. penalty. If you have any questions, feel free to contact me.
If I am not in my office or on campus,
call me at home at 410-871-9580. Good luck!
[10 pts.] 1. Profit Function
Consider the profit function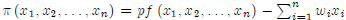
. Prove that a
sufficient
condition for concavity of the profit function is concavity of the production
function .
[25 pts.] 2. Labor/Leisure Choices
In previous utility-maximizing situations, we have assumed that money income is
exogenous. In the real world ,
however, this is not the case. For more individuals, their income is at least in
part a function of how much they
work. That is,
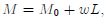
where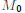 
represents non-wage income, w the wage
rate, and L hours worked, the quantity wL represents labor
income. The household budget constraint is thus
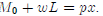
For this to be a non-trivial problem, we must incorporate labor decisions into
the utility function. Suppose that our
utility function was additively separable in consumption and labor, that is we
could write U(x, L) = u(x)+v(L),
where u is well-behaved (i.e. is concave) and v has properties v < 0, v' < 0,
v'' < 0. The intuition here is that
having to work gives an individual disutility and that the marginal disutility
of work is increasing.
(a) Write down the Lagrangian for this problem and take the first- order
conditions .
(b) Totally differentiate the first -order conditions and use Cramer’s rule to
find the comparative statics
derivatives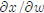 
and
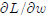. If possible, sign these derivatives.
(c) Redo part (b), only now you are looking for
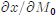and 
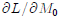. If
possible, sign these derivatives.
(d) If u(x) = θ log x and v (L) = -L2/2, solve this system for the
optimal quantities x* and L*: [HINT:
You will find the quadratic formula helpful. Recall that the quadratic formula
tells us that the roots to the
second-degree polynomial ay 2 + by + c are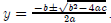
]
(e) You know that x* is a demand function. Provide an analogous interpretation
for L* .
[15 pts.] 3. Constant Elasticity of Substitution Utility
Consider the utility function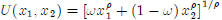 
(ρ and ω
are constant parameters).
(a) This is a special preference specification called the constant elasticity of
substitution (CES) utility function.
The elasticity of substitution is defined as: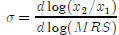 
,
it measures the curvature of an indifference
curve. Verify that the elasticity of substitution is indeed constant for this
utility function. Use the following
steps :
(i) Find the Marginal Rate of Substitution for this utility function. Recall
that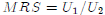 
. The
MRS should be a function of the ratio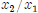 
.
(ii) Take logs and differentiate , do note be confused by the notatation. If we
let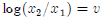 
and
log(MRS) = w, you are deriving dv/dw:
(b) Write down an appropriate budget constraint, form a
Lagrangian, and solve for the demand functions.
[25 pts.] 4. Profit Maximization
Do problem 14 from Chapter 4 of the Silberberg and Suen text. You may skip parts
(c), (f), (h) and (i).
[25 pts.] 5. Monopoly and Elasticities
Consider a monopolist that faces the inverse demand curve p(y): If the
monopolist’s cost function is denoted
c(y), its profit function is:
π(y) = p(y)y - c(y).
(a) Take the first- and second- order conditions for the monopoly problem.
(b) The monopoly price is can be expressed as:
p(y) = g(y)MC(y),
where MC denotes marginal cost and g(y) > 1 it the markup over marginal cost.
Use the first-order
condition to show that the markup is a function of the elasticity of demand,
.
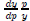(c) Show that the markup is constant for the isoelastic demand function y = Apb
(d) Using your answers to (b) and (c), explain in math and in English why a
monopolist will always produce at
a point such that the demand for its good or service is elastic. [HINT: Show
what happens to total revenue
if output falls and demand is inelastic.]
