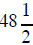We add and subtract fractions with a common
denominator using the following rule. If there is a
common denominator then combine the numerators and put them over that common
denominator.
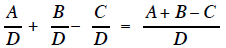
This process could be written backwards and still be
a true equation .
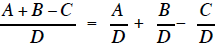
This rule states that if we have a polynomial with
several terms in the numerator of a fraction then we
can break that fraction into several separate fractions. Each of the separate
fractions will have one term
of the polynomial in the numerator and the common denominator in the
denominator.
The quotient rule can be used to reduce fractions
but the numerator and denominator must both be
monomials. The quotient rule cannot be used if the numerator or denominator has
more that one term.
We CANNOT cancel parts of the polynomial.
You cannot reduce the parts
of addition or subtraction |
You can reduce if everything
is a factor |
 |
 |
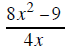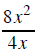the 4 and the 8
and x the and the x^2
cannot be reduced |
the 4 and the 8
and x the and the x^2
CAN be reduced |
If the denominator of the fraction is a monomial
then you break up each fraction into its separate parts
and then each separate fraction can be reduced using the quotient rule.
| Example 1 |
Example 2 |
Example 3 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
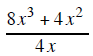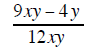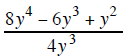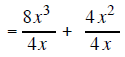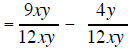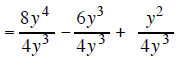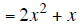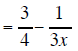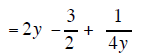Dividing Polynomials if the denominator is a Binomial:
Long Division
Why breaking up the fraction with a binomial in the denominator will not work.
Breaking up a fraction into its separate parts and
using the quotient rule to reduce each separate
fraction will not work if the denominator is a binomial. If we did break up the
fraction then each separate
fraction would have the binomial as their denominator.
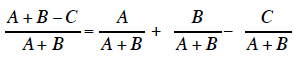
The quotient rule cannot be used to reduce each
separate fraction if the numerator and denominator are
not both monomials. We must develop another process to reduce the fraction. The
process we use
is to divide the binomial in the denominator into the numerator by using long
division. This long
division process will look like the long division process for fractions with
whole numbers that you have
used in the past. The process will be a bit more involved due to the nature of
the algebraic terms
involved.
Long division with whole numbers
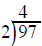divide the 2
outside into the first number inside (9) and put the results over the 9
multiply the 4 on top by the 2 outside and write the product 8 under the 9
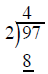multiply the 8 in the
new row by −1 to create a subtraction problem
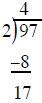combine the terms above
the underline and bring down the 7
Start the process over again
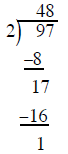
Divide 2 into 17 to get 8. Put the 8 above the 7 and
multiply the 2 and 8. Put the 16 under the 17 multiply the 16 in the new row by
−1 to create a subtraction problem We are done and have a remainder of 1 the
answer is
