OBJECTIVES
• Understand function as an object
• Transformations and families of functions
FUNCTION AS AN OBJECT (Chapter 1: Sections 1-3 through 1-5)
The concept of function as an object that we can do things to is central to
the study of algebra.
We treat a function as an object when we
• Classify functions as having properties, such as: symmetry about the
y-axis or symmetry
about the origin
• Transform functions by adding or multiplying constants within a
function to move or
change the shape of the graph of the function
• Perform algebraic operations on functions, such as: adding,
subtracting, multiplying,
dividing , and taking the composition of functions
• Find the inverse of a function
In this lab we will focus on the study of functions as objects by exploring the
transformation of
functions. There are three types of transformations of function graphs that
allow us to graph a
myriad of related functions for known basic functions. To do this we must first
recognize the
shape of the known basic function graphs. We can then use symmetry to aid in
sketching the
graph. In addition, we need to understand the related function concepts of
domain and range.
SEVEN BASIC FUNCTIONS
In order to apply a transformation to a function, we must know what the original
function looks
like. So we will begin by graphing seven basic functions and determining their
domain, range,
and symmetries.
The software tool we use for this lab is a dynamic
graphing utility called Grapher.
We will do the basic linear function f(x) = x as an
example.
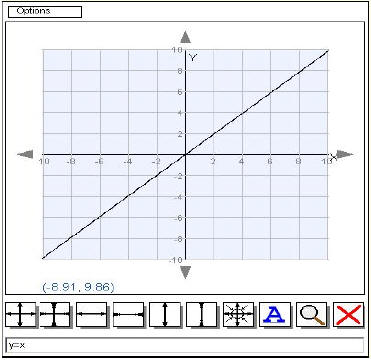
EXAMPLE 1: Determine the shape, domain, range,
and any symmetry for the basic linear
function f(x) = x.
SOLUTION :
A. Enter the function f(x) = x in Grapher on the entry line as y=x (Grapher
does not recognize
function notation, so we will write the functions in equation notation).
Press the ENTER KEY to
plot the function. The result is the graph in Figure 1 below.
B. We determine the domain by examining the x-axis and asking for what
values of x does the
function assign a y value? For this linear function every x is assigned
a y-value so the domain is
all real numbers. In interval notation we write this as Domain of f(x) =
(-∞, +∞).
C. We determine the range by examining the y-axis and asking for what
values of y does the
function have a related x value? Again for this linear function the
range is all real numbers. So
in interval notation the Range of f(x) = (-∞, +∞).
D. Finally we ask if the function is symmetric to the y-axis or the
origin. If a function is
symmetric to the y-axis then it reflects about the y-axis. Think of
the y-axis as being a mirror
that reflects the right side onto the left. For f(x) = x the line is not
mirrored in the y-axis, so the
function is not symmetric with respect to the y-axis. If a function is
symmetric to the origin
then a half-turn centered at the origin will place the graph back on top
of itself. A half-turn of
the basic linear function does place the graph back on top of itself, so
the function is symmetric
to the origin. |
Figure 1: Plot of f(x) = x
Can you see why we would never need to check a function
for symmetry about the x-axis? Now
let’s explore the properties of the six remaining basic functions.
Exercise 1: Use Grapher to graph the
remaining six basic functions in Table 1 and complete Table 1 by
determining the domain, range, and symmetry for each function. Write the
domains
and ranges in interval notation (see Section 1.4 for help on interval
notation). |
Table 1: Basic Function Properties
| Basic Function |
Domain |
Range |
Symmetry |
Constant Function:
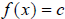
Grapher enter y=5 as an example |
|
|
|
Linear Function:
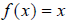
Grapher enter y=x |
(-∞, +∞) |
(-∞, +∞) |
Origin |
Square function:
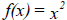
Grapher enter y=x^2 |
|
|
|
Cube function:
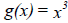
Grapher enter y=x^3 |
|
|
|
Square root function:
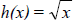
Grapher enter y=sqrt(x) |
|
|
|
Absolute value function:
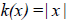
Grapher enter y=abs(x) |
|
|
|
Reciprocal function:
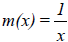
Grapher enter y=1/x |
|
|
|
TRANSFORMING BASIC FUNCTIONS
Now that you know the properties of some basic functions and the shape of their
graphs, we can
examine transforming the basic functions. A transformation of a graph occurs
when we add or
multiple a real number within the function. For example, the basic linear
function f(x)=x can be
transformed into f(x)=ax+b by multiplying x by a real number a and/or adding a
real number b.
The result of such transformations is a change in the graph of the function. We
are going to
explore the effects of different transformations .
Exercise 4: Clear the graph from Exercise
3 and reset the window to 10 x 10.
A. Let the base function be 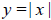 . In the
Grapher type y = abs(x+b) and press the ENTER Key. Examine for . In the
Grapher type y = abs(x+b) and press the ENTER Key. Examine for
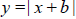 for b= -10 to 10. Describe the
transformation that results from adding inside the base function
(in essence, we are adding b directly to the x variable). for b= -10 to 10. Describe the
transformation that results from adding inside the base function
(in essence, we are adding b directly to the x variable).
B. Does it work the same for other base functions? Try some. |
Exercise 5: Clear the graph from Exercise
4 and reset the window to 10 x 10.
A. Let the base function be 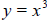 . In the
Grapher type y = x^3+c and press the ENTER Key. Examine . In the
Grapher type y = x^3+c and press the ENTER Key. Examine
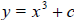 for c = -10 to 10. Describe the
transformation that results from adding c outside the base function (in
essence, we are adding c to the entire base function, or y variable). for c = -10 to 10. Describe the
transformation that results from adding c outside the base function (in
essence, we are adding c to the entire base function, or y variable).
B. Does it work the same for other base functions? Try some. |
COMBINING TRANSFORMATIONS
If we perform more than one transformation at a time, the order they are
performed in is
important. In y = a· f(x+b)+c, if the c transformation is performed before the a
transformation
the graph will not be the one intended. Indeed, the graph would be of y = a· [f(x+b)+c],
which
is not equivalent to the original function. This situation is avoided by
following the simple rule:
given a function written in the form y = a· f(x+b)+c, always perform
the “a”
transformation before the “c” transformation. Any other order except this
may result in a
non-equivalent or incorrect transformation.
Exercise 6: Let’s combine all the above
work to sketch the graph of a function that is the result
of multiple transformations of a base function.
A. 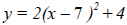 For what is the basic function
being transformed? For what is the basic function
being transformed?
B. Before you use Grapher to graph the function
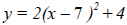 , determine the effect of the , determine the effect of the
three transformations performed on this base function.
C. Use Grapher to graph the function 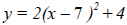 .
Does the graph match your predictions from Part 6B? If not, make
corrections. .
Does the graph match your predictions from Part 6B? If not, make
corrections. |



