Electronic submission of homework assignments is strongly encouraged for the
computer problems. For
the written part, you are encouraged (but not required) to typeset using LATEX
or LYX (an easy-to-use
front-end of LATEX). For electronic submission, homework is due at 11.59pm on
the due date. For paper
submission, homework is due in class on the due date.
0. (0 points) This exercise is for you to get familiar with the computing
environment. Unless you are
proficient in setting up your own computer, you are urged to use the Linux (not
Windows) computers
at the Mathlab SINC Site in Math Tower S-235 to do all your computing
assignments. Before you can
log-on to the computers at the SINC site, you may need to go to the Mathlab SINC
site in person
to activate your account on any of the Linux system by following the on-screen
instructions. After
you log in , make sure you can run emacs (for editing), gv (for viewing eps
files), and ddd (for debugging).
If you have a personal computer, after activating your Mathlab account you
can remotely log onto the
computer “compute.mathlab.sunysb.edu” from your PC. You need an ssh client and
XWindows server
on your local computer (available on Linux, Mac OS X, and Cygwin on Microsoft
Windows). You can
remotely log onto the computer using command where username should be changed to
your own username, and -X and -Y options would ensure X Windows applications can
be displayed on your local computer. After you remotely log onto the computer,
try to run gv, ddd, and emacs and make sure the windows are properly displayed
on your local
computer. Practice using scp to copy files between you local and remote
computers.
1. (25 points)
(a) (5 points) Use the given C program hw1_1a.c to compute an approximate
value for the derivative
of a function using the finite difference formula
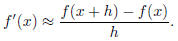
The program uses the test function tan(x) for x = 1, and determines the error
by comparing with
tan (x)2 + 1. It prints out the magnitude of the error for h = 10-k, k = 0,
. . . ,
16, and plots the
magnitude of error as a function of h using log scale.
Read the program and follow its instruction to compile and
run it. What is the minimum value
for the magnitude of the error? How does the corresponding value for h compare
with the “rule
of thumb”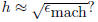
(b) (10 points) The given program uses double- precision
floating point numbers . Edit the program in
an editor (such as emacs) and modify the program to use single-precision
floating point numbers.
Perform the same test, plot the results, and answer the two questions in part
(a).
(c) (10 points) Modify the program to use the centered
difference approximation
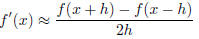
and repeat the same test as in (a) using both
double-precision and single-precision floating point
arithmetic.
For each part of the problem, turn in the modified part of
the program, the plots, and your
explanations of the results.
2. (15 points) Starting from the code template hw1_2.c,
complete the program to generate the first 60
terms in the sequence given by the difference equation
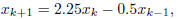
with starting values
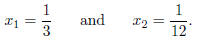
Make a semi-log plot of the values you obtain as a
function of k. The exact solution of the difference
equation is given by
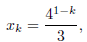
which decreases monotonically as k increases. Does your
graph confirm this theoretically expected
behavior? Explain your results. Turn in the modified part of the program, the
plots, and your
explanations of the results.
3. (25 points) To solve the quadratic equation ax2
+ bx + c = 0, one can use the standard quadratic
formula
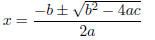
or the alternative formula
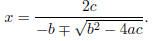
(a) Show that the alternative quadratic formula indeed
gives the correct roots for the quadratic
equation (assuming exact arithmetic ). When the standard quadratic formula would
be more
accurate than the alternative formula and vice versa using floating point
arithmetic?
(b) Use the given sample C program hw1_3b.c for the
standard quadratic formula to solve the
quadratic formula for the following coefficients in the following table. Fill
the solutions into
the table.
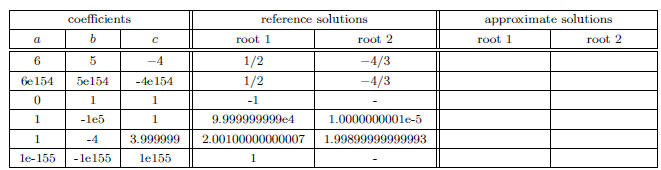
(c) Enhance the robustness of the code to guard against
i. division by zero ,
ii. unnecessary overflow and underflow (e.g., by scaling the coefficients), and
iii. cancellation (e.g., by using alternative formula when appropriate).
You do not need to handle complex roots . Produce a similar
table as in part (b). Turn in your
modified part of the program, a description of your changes, and the tables.



