Algebra I : Symbolic reasoning and calculations with
symbols are central in algebra. Through the study of
algebra, a student develops an understanding of the symbolic language of
mathematics and the sciences. In
addition, algebraic skills and concepts are developed and used in a wide variety
of problem-solving situations
a. Fill in the blanks below with a single appropriate
letter to identify each set of
numbers with the properties or descriptions of the elements which characterize
that set:
The set of:
E Even Numbers
D Rational Numbers
G Irrational Numbers
C Real Numbers |
B Integers
F Odd Numbers
J Natural Numbers
H Whole Numbers |
A. any number equal to a terminating decimal expression
B. {..., -3, -2, -1, 0, 1, 2, 3, ...}
C. any number which is rational or irrational
D. any number of the form 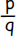 where p and q are
integers and q is not zero
where p and q are
integers and q is not zero
E. any integer of the form 2k, where k is an integer
F. any integer of the form 2k + 1, where k is an integer
G. any number equal to an infinite decimal expression with no repeating block of
digits
H. {0, 1, 2, 3, ...}
I. any number which can be expressed as a ratio
J. {1, 2, 3, ...}
b.
Which of the following sets of numbers are not closed under addition?
__ The set of real numbers  __ The set of
rational numbers
__ The set of
rational numbers

 The set of irrational numbers __ The set of
positive integers
The set of irrational numbers __ The set of
positive integers
2.0: Students understand and use such
operations as taking the opposite, finding the reciprocal,
taking a root , and raising to a fractional power . They understand and
use the rules of exponents. |
a. Which number below is the same as
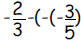 ?
?
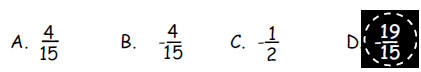
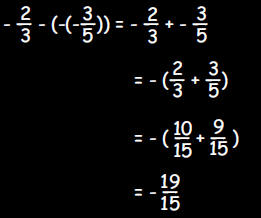
b. What number z satisfies the equation
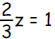 ?
?
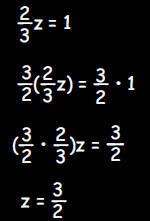
c. Calculate and simplify the expression
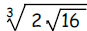

d. If x = 4, what is 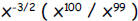
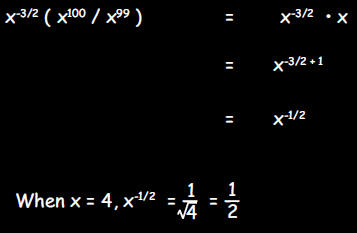
e. Write 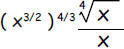 as x raised
to a power
as x raised
to a power
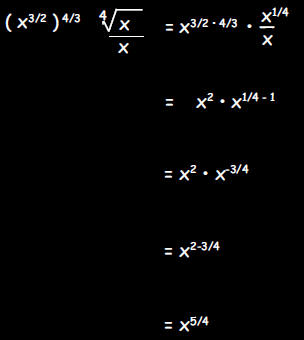
a |2x - 1| = 5 Find all values of x which make this
equation true
If |2x - 1| = 5, then 2x - 1 = 5 or 2x - 1 = -5
Therefore x = 3 or x = -2 |
b. 3|2 - 5x| + 1 < 10 Find all values of x which make this
inequality true

Solution: All numbers greater than
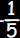 and less than 1 and less than 1 |
c. 4|x - 1| = 16 Find all values of x which make this
equation true
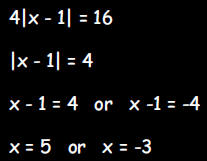
d. |x- 2| > 4 Find all values for x which make this
inequality true
Either x - 2 > 4 or x - 2 < - 4
Either x > 6 or x < -2
Solution: All numbers less than -2 or greater than 6 |
4.0: Students simplify expressions before
solving linear equations and inequalities in
one variable, such as 3(2x-5) + 4 (x-2) = 12. |
a. Simplify
1. 3 ( 2x - 5 ) + 4 ( x - 2 )
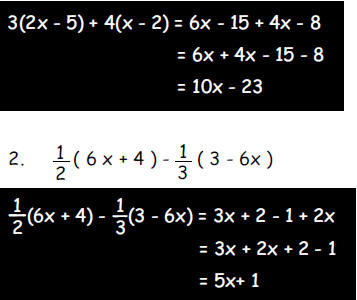
b. Solve for x
1. 8(x + 1) + 3(2x - 2) = 44
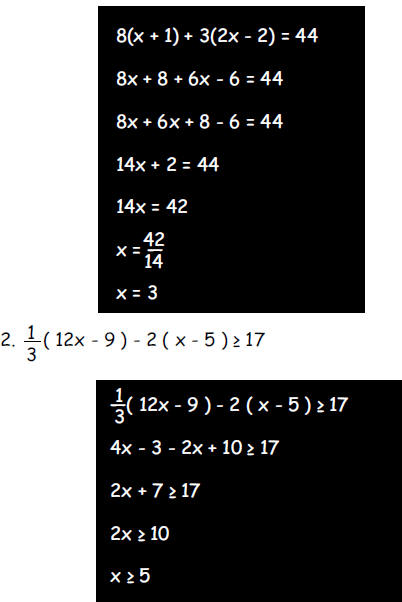
5.0: Students solve multi-step problems,
including word problems, involving linear
equations and linear inequalities in one variable and provide
justification for each step. |
a. Justify each step below for the solution for x from the
equation
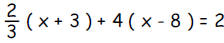
Use the following list:
A. Commutative Property of Addition
B. Associative Property of Addition
C. Commutative Property of Multiplication
D. Associative Property of Multiplication
E. Distributive Property
F. adding the same quantity to both sides of an equation preserves equality
G. multiplying both sides of an equation by the same number preserves
equality
H. 0 is the additive identity
I. 1 is the multiplicative identity
To the right of each equation below (and on the following pages) where there is
an
empty space, write one of the letters 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', or
'I' to justify
how that equation follows from the one above it. For example, the second
equation
below is justified by 'G' and the third one by 'E'.
|
Step
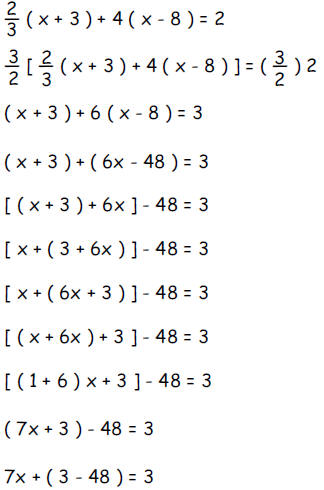
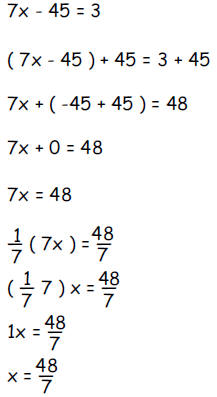 |
Justification The given equation

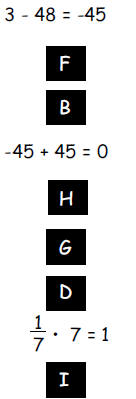
|
b. The sum of three integers is 66. The second is 2 more
than the
first, and the third is 4 more than twice the first.
What are the integers?
Let x be the first number. The the second number is x + 2 and the
third number is 2x + 4.
x + (x + 2) + (2x + 4) = 66
4x + 6 = 66
4x = 60
x = 15
x + 2 = 17
2x + 4 = 34
The three numbers are 15, 17, and 34 |
c. During an illness, a patient's body temperature T
satisfied the inequality
|T - 98.6| ≤ 2. Find the lowest temperature the patient could have had during
the
illness.
|T - 98.6| ≤ 2
-2 ≤ T - 98.6 ≤ 2
-2 + 98.6 ≤ T ≤ 2 + 98.6
96.6 ≤ T ≤ 100.6
The lowest temperature the patient could have had is 96.6 |
6.0: Students graph a linear equation and
compute the x- and y-intercepts (e.g., graph
2x + 6y = 4). They are also able to sketch the region defined by linear
equality (e.g.,
they sketch the region defined by 2x + 6y < 4). |
a. Graph the equation: 2x - y = 3

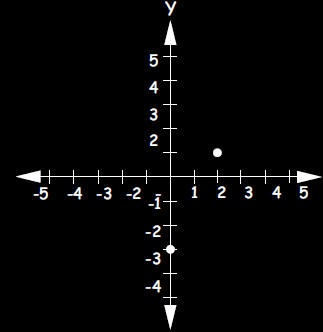 |
Two points on the line are
(0,-3) and (2,1). Note: Two
points determine a line.
Calculating the coordinates of
any two points on the line
determines the same graph.
|
b. What is the x intercept?
|
In the equation 2x - y = 3 (or y = 2x -3), substitute y = 0.
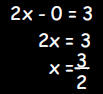 |
c. What is the y intercept?
In the equation 2x - y = 3, substitute x = 0 to get y = -3.
Alternatively,
since b is the y intercept for y = mx + b, it
follows that -3 is the y intercept for y = 2x -3. |
d. On your graph, mark the region showing 2x - 3 < y
The shaded
region shows
2x - 3 < y |
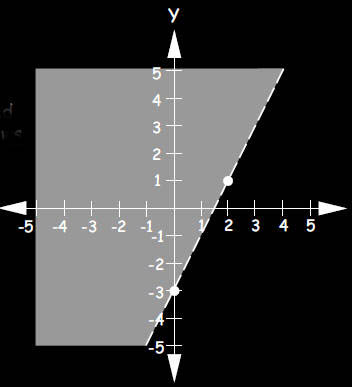 |
| |



