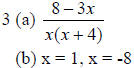A rational equation is an equation that involves
one or more rational expressions. For example,
the equation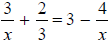 
is a rational equation.
To solve a rational equation, the denominators can be
eliminated by multiplying each side of the
equation by the LCD of all of the rational expressions in the equation.
The steps are:
1. Determine the LCD of all of the rational expressions in the equation .
2. Multiply each side of the equation by the LCD.
3. Use the distributive law so that each individual expression is multiplied by
the LCD.
4. Simplify by dividing out common factors.
5. Solve the resulting equation.
6.
Check the answer(s) in the original equation. This is very important because it
is
possible to find a solution for the equation in step #5 that is not a solution
of the original
equation. This happens if the value found in step #5 makes one or more of the
denominators of the original equation equal to zero .
1. Use the steps given above to solve each of the following equations. For each
equation,
first write down the LCD.
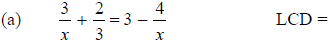
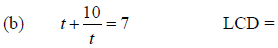
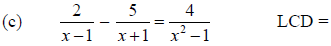
2. Let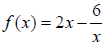 
. Find all
values of a such that f (a) =1.
3. Summary :
The LCD (least common denominator) is used when adding or subtracting rational
expressions
and when solving rational equations.
When the LCD is used in adding or subtracting rational expressions, the
numerator and
denominator of each fraction must be multiplied only by the factors that are
necessary to turn the
denominator into the LCD. That is, compare each denominator to the LCD and then
multiply
both the numerator and denominator of that fraction by the factors in the LCD
that are missing
from that denominator.
When the LCD is used in solving rational equations, multiply the entire
left side and the entire
right side of each equation by the LCD. This will result in each term being
multiplied by the
LCD. If the LCD has been chosen correctly, each fraction in the equation can
then be reduced
and the new equation should contain no fractions. Remember that it is very
important to check
your answer or answers in the original equation since extraneous solutions might
be obtained.
Keeping these guidelines in mind, add, subtract, or solve as indicated.
(a) Subtract:
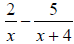
(b) Solve:
Answers
1.
(a) x = 3
(b) t = 2, t = 5
(c) No solutions
2. a = -3/2, a = 2
