We begin this lesson with a summary of common graphs that
we have seen thus far. We have already had experience with constant and linear
functions , and have been introduced, albeit sparingly, to the other graphs.
Nevertheless, these are very common functions and it is necessary to be able to
recognize them by sight.
For example, we know that linear functions of the form
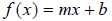all have one common feature: Their graphs
are lines. Instead of tediously plotting points to generate a graph, we use the
fact that this graph has a slope m and a y- intercept of b . These bits of
information serve as convenient shortcuts toward plotting a line. We will use
similar ideas with more complex graphs.
One of the simplest graphs is the parabola
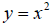. On your calculator, enter this function in
your function editor. Graph it on the standard window. Now type in the function
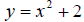and graph it. You will notice that this
graph is exactly the same as the first graph, only in a different location . In
particular, each y-value from the original function has been increased by 2 in
the new function. Hence, the effect of the “+2” was to shift the original graph
up two units . This is an example of a vertical shift. What do you think the
graph of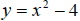 
looks like ?
Clear out your graphs except for the
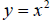graph (we keep this one on the screen for
comparison purposes ). Now type in this function:
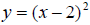, and graph it. This graph is the original
graph now shifted to the right two units. This may be counterintuitive, but try
this: If you set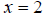 
, you will note that
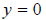. The x-intercept is at (2,0), shifted two
units to the right from the original graph. This is a horizontal shift.
We summarize:
Given any function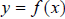 
,
a)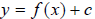 
represents a
vertical shift of f(x), that is, the original graph has been shifted up or down
c units. Specifically, up c units if c is positive, down c units if c is
negative.
b)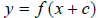 
represents a
horizontal shift of f(x).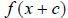
shifts c units to
the left if c is positive, or c units to the right if c is negative. You will
have to train your mind to remember that the horizontal shift is opposite the
sign in front of the c.
Note: it is common to use the letter k for vertical shifts
and the letter h for horizontal shifts. Therefore, it is easy to read the
expression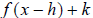 
as the function f(x) shifted h
units left or right, and k units up or down. Also, the negative in front of the
h lends an intuitive sense to the expression. For example,
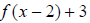means the function has been shifted 2 units
to the right, or read as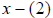 
, and 3 units down.
Now go back to your calculator and enter
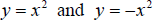, and graph them. You will notice the second
function is reflected across the x-axis, although the shape of the original
graph has not changed. In general, given a function
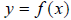, its horizontal reflection across the x-axis
is found by negating the entire function, or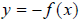 
.
Its vertical reflection across the y-axis is found by negating the input value
before evaluating, or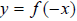 
.
These two reflections can be combined as such:
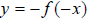, in which both reflections take place. This
has the same effect as turning the graph upside down from its original position,
or literally, turning your sheet of paper 180 degrees.
Reflections and shifts are called rigid transformations
since they do not change the shape of the original graph, only its location and
orientation. A non-rigid transformation changes the shape of the original graph,
and an example of a non-rigid transformation is found by multiplying the
original function by a constant (but not 0). Experiment on your grapher by
graphing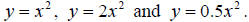 
The effect of the coefficient 2 in
the second graph is to “stretch” the original graph upwards, making it appear
taller, while the coefficient 0.5 “shrinks” the original graph, making it appear
squatter (or, equivalently, stretches it in the horizontal direction).
Remember, the purpose of shifts, reflections and
stretches/shrinks is to aid you in graphing functions. You should not have to
plot many points at all. You should be able to determine the function’s basic
shape and then apply these transformations to the graph to arrive at your
answer.
Combinations of Functions
We discuss the arithmetic of functions. Given two
functions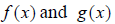 
, you can add, subtract , multiply
and divide these functions as you please, as long as you follow sound algebra
techniques. Also note the convenience of using function notation. We can write
the sum of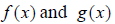 
as a new function whose name is
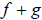and written
.
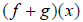When performing division , please note which values of x
cannot be used, and restrict your domain accordingly.
Composition of functions, is an extremely important
operation of functions. Given two functions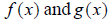 
,
we can create the new function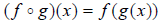 
, which reads
“function f evaluated at g(x)”. You are literally inserting g(x) into the
variable x in the function f(x). The new function is often referred to as “f
comp g”.
Normally,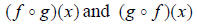 
are not
equal. We will see in the next section that composition is a useful tool for
determining whether two functions are inverses of one another. Study the algebra
involved in simplifying these expressions, and be especially cognizant of the
meaning of the variables, and of the final composition function.
Generally, you should find the resulting composition
function first before evaluating at a value of x. For example, if you were asked
to evaluate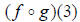 
, you would want to find
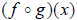first, then insert the 3. Composition simply
requires practice.
Inverse Functions
Lastly, we discuss the inverse of a function. Intuitively,
the inverse “undoes” the actions of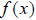 
. Suppose
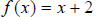. Then, 
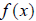generates points such as (1,3), (2,4), (3,5), among many possibilities, simply
by arbitrarily picking an x-value, and evaluating for its corresponding y
value.. The inverse of 
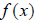would consist of the
points (3,1), (4,2), (5,3), or the transpose of any point found by
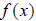. For now, we will denote the inverse of a
function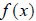 
by the notation
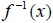, read as “f-inverse”.
We need to discuss many facets regarding inverse
functions. First, let us discuss the inverse graphs of functions. Since the
inverse graph switches the order of the x and y values in each coordinate, the
inverse graph appears as a mirror image across the 45-degree line.
However, some inverse graphs are not functions themselves.
Let us discuss the conditions for the existence of an inverse function.
Let us consider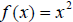 
. As an
example,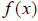 
generates points such as (2,4) and
(-2,4). The inverse of 
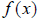would contain the
points (4,2) and (4,-2). However, the inverse graph would NOT be a function,
since the input value of 4 returns two output values for y, and this is NOT
allowed for a function! Therefore,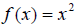 
does not
have an inverse function. A graph of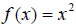 
shows
that there are y-values that have more than one x-value corresponding to it.
This is acceptable, but when we reverse the order of the coordinates, this
produces a graph that fails the VLT.
The horizontal line test (HLT) is a visual test in which
you visualize horizontal lines over the graph of
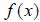. If there exists a horizontal line that
intersects the graph more than once, then the inverse function will not exist.
On the other hand, if no horizontal line intersects the graph more than once,
the graph of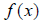 
“passes” the HLT, and
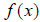is said to be “one-to-one,” and the inverse
function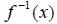 
exists. See page 149 for examples
of the use of the HLT.
To verify whether two functions are inverses, form the
composition of the two functions. If the two functions are inverses of one
another, both of their compositions will simplify to “x.”
Once you have determined that a function
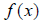has passed the HLT and its inverse function
exists, then you need to find it. This is a three- step process :
1. Rewrite the function using y in place of
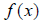. This is done purely for convenience.
2. Switch the x and y variables. Leave everything else unchanged.
3. Solve for y . The result is the inverse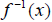 
.
To summarize:
Every function’s graph has an inverse graph, but the inverse graph itself may
not be a function. Equation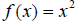 
is an example.
Its inverse graph fails the VLT, so there does not exist a
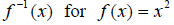. Note: we can get around this conundrum by
restricting the domain on the original 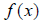in
such a way that the graph is one-to-one. Hence, for
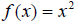, we often limit x to the domain
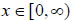, which essentially cuts the original
parabola in half . The remaining “half” is a one-to-one function, and its inverse
is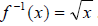 
If 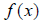passes the HLT, its
inverse is a function, denoted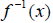 
. To find the
inverse function, switch x and y and solve again for y.
If given two functions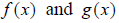 
,
you can show if they are inverse of one another by verifying that and that
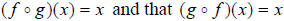as well..
