| Teaching Actions |
Comments |
| Warm Up
Tom was in a hurry when he was doing his homework.
He has a picture that is partially drawn. What number
is shown on the number line?

Large Group Introduction
1. Remind students that they are able to add
fractions
using fraction circles and with symbols . Explain
that in this lesson, they will see how to model
adding and subtracting fractions on a number line.
2. State clearly that the goal is for them to
explain how
to use a number line to model fraction addition and
subtraction.
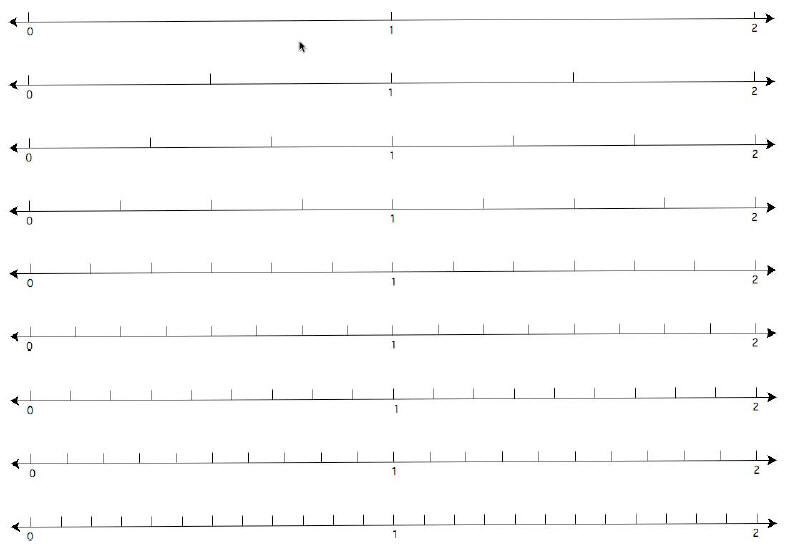
3. Direct students’ attention to the 6 number
lines on
the board. Students should have Student Page A
showing the same number lines.
Ask: How are these number lines alike and
different? |
The purpose of this lesson is to
reinforce students’ understanding of
the addition and subtraction
procedure for fractions by making
symbolic to picture translations using
the number line as the picture.Students
understanding of the
algorithm for adding and subtracting
fractions is strengthened by asking
them to make sense of adding and
subtracting on a number line.
Students use the algorithm to made
sense of this new model. Consider
what the students will need to do to
use the number line to add and
subtraction fractions:
• The decision as to what number
line to use to add or subtract two
fractions is equivalent to finding
common denominator.
• Identifying each fraction as an
equivalent amount on the
number line relies on students’
ability to find equivalent fractions
symbolically.
Students should note that the lines
are equal in length; the distance from
0 to 1 is the same. The lines are
partitioned into different number of
equal parts. |
4. Present this story problem: Jacob
ran 2/3 of a mile
and stopped to tie his shoelaces. He then ran
another 1/2 of a mile. Did he run more or less than
one mile?5. Estimate: Is the amount > or <
1? Greater or less
than 2? More or less than 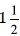 ? ? |
|
6. Show the ribbons cut into 2/3
length and 1/2 length.
Place the ribbons on the first number line (no
fractional amounts shown). Mark the spot on the
number line that shows the length of the two
ribbons combined .7. Comment on their
estimate. Ask: What is the exact
amount? You know how to do this with fraction
circles. You know how to do this with symbols.
Now you need to figure out how to model this on
the number line.
8. Ask: Which number line might be the best one to
show how much Jacob ran in all? Try their
suggestions. Ask students to explain their
reasoning.
9. Move the ribbons to the number line partitioned
into sixths. Ask: 2/3 is equal to how many 6ths? 1/2 is
equal to how many 6ths? What is the total number
of miles that Jacob ran?
10. Ask: Why is the 6ths number line better for
solving
this problem than the number line showing 3rds?
(Both fractions can be easily modeled on the number
line showing 6ths).
11. Ask: How might you use symbols to show what
you
did on the number line?
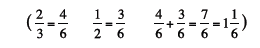 |
Prepare 2 lengths of ribbon. One is
2/3 the length of the unit of the
number line you drew on the board.
The other is 1/2 the length of the unit.You
may want at this point to step
back and let students try to do this on
their own as opposed to guiding
them through the steps.
The idea is for students to build on
their prior experience with
equivalence and operating with
fractions and symbols to see that the
number line representing the
common denominator is the best
choice. For example a student
working on 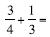 explained that he explained that he
would use the “12 number line
because they both go into it.”
Number line for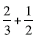
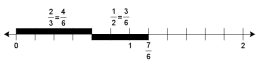 |
12. Repeat for
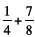 13. Ask:
In what ways is adding fractions using the
number line the same as using fraction circles? How
is it the same as using just symbols?
14. Suggest that they imagine adding
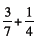 using a using a
number line. Ask: What type of number line would
you need to add these two fractions ? |
|
| Small Group/Partner Work
15. Provide practice using Student Pages B -H. As
students work on these problems, stop by each
group and ask students to explain what they are
doing.
16. Student Pages F- H ask students to construct
for
themselves a way to model subtraction on the
number line. On the first story problem students
may draw in two lines and compare lengths; on the
take away problem, students may draw one line and
count back. |
Students will need extra copies of the
number lines (Student Page A). As
you watch students do the class work
notice if they are labeling the number
lines. If not, encourage students to
label the number lines to clearly show
the numbers involved.Take away model on the
number line
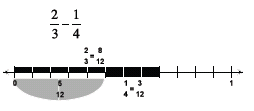
|
| Wrap Up
17. End class by sharing students’ strategies for
subtraction.
18. Help students to verbalize how finding answers
on
the number line is the same as adding or subtracting
finding common denominators . |
|
Translations:
• Real life to verbal to pictures to symbols
• Symbols to pictures to symbols
Tom was in a hurry when he was doing his
homework. He has a picture that is
partially drawn. What number is shown on
the number line?
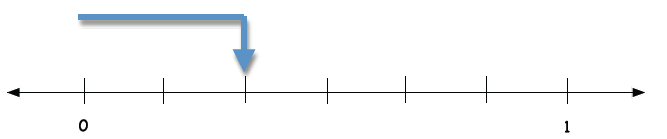
Post Lesson Reflection
Lesson_________________
1) Number of class periods allocated to this lesson: ______________
2) Student Pages used: __________________
3) Adaptations made to lesson: (For example: added extra examples, eliminated
certain problems, changed fractions used)
4) Adaptations made on Student Pages:
5) To improve the lesson I suggest:



