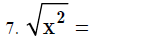Using only integers, we do not have a number to describe
dividing one whole pie into
four equal pieces. The rational numbers were created to solve this problem.
A RATIONAL NUMBER is a number that can be represented as a
ratio of two integers
a/b for any integer a and any nonzero
integer b
Note that “a over b” and “a divided by b” mean the same
thing, solving the “division
problem” is built into the definition of a rational number!
Note also that every integer is also a rational number
since an integer z can also be
expressed as z/1 “z divided by 1”.
Now that we know what a rational number is, how do we add,
subtract, multiply and
divide them?
ADDITION and SUBTRACTION
Adding and Subtracting Fractions:
o Find a least common denominator using method for LCM
o Change the numerators of each fraction
o Add or subtract the numerators (keep denominator unchanged)
o Reduce
Examples:
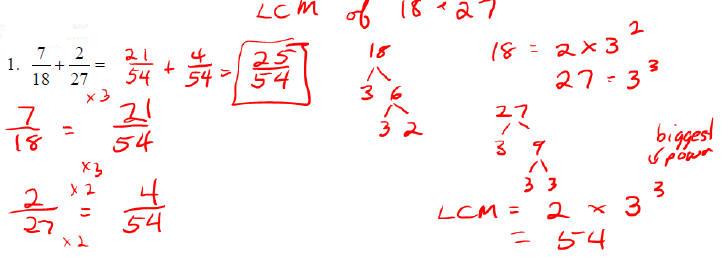
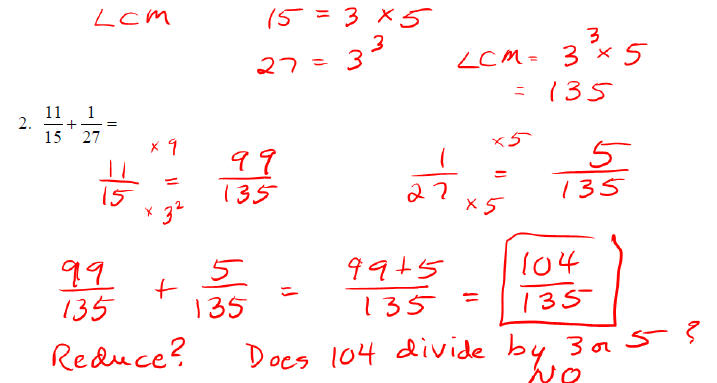
MULTIPLICATION and DIVISION
Multiplying Fractions:
o Simplify the fractions if not in lowest terms .
o Multiply the numerators of the fractions to get the new numerator.
o Multiply the denominators of the fractions to get the new denominator.
Examples:
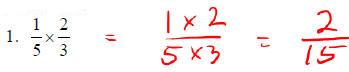
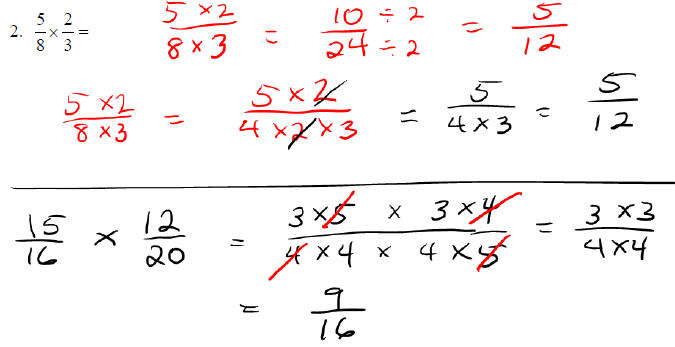
Dividing Fractions:
o Multiply the first fraction by the reciprocal of the second
Examples:
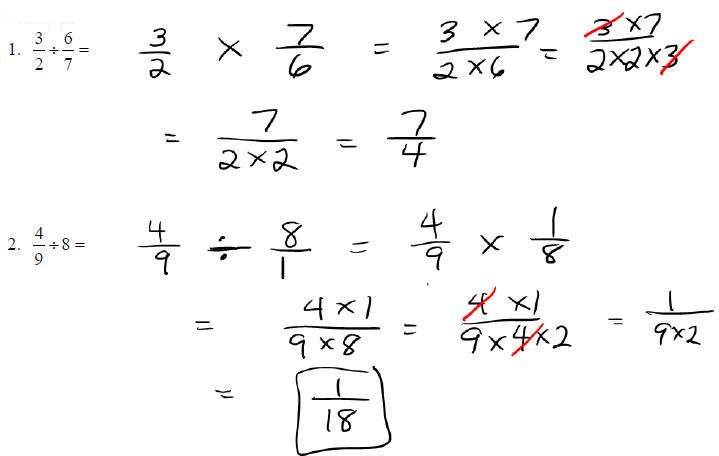
POWERS – SHORTHAND for multiplication and division
Define
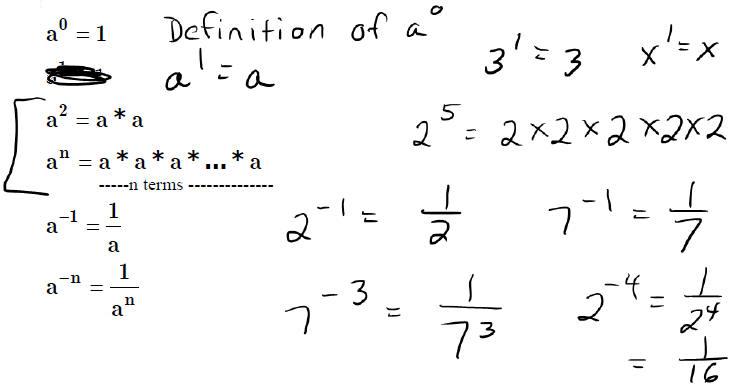
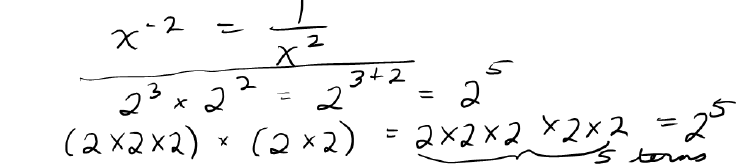
Rules for multiplying and dividing with exponents:
Rules for Exponents:
| • Multiplying Powers: |
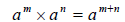 |
| • Dividing Powers: |
 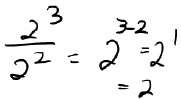 |
| • Negative Powers |
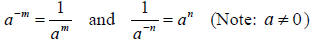 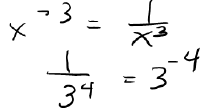 |
| • Zero Power Rule : |
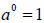 |
| • If no power is shown, then the exponent is 1. |
|
Examples:
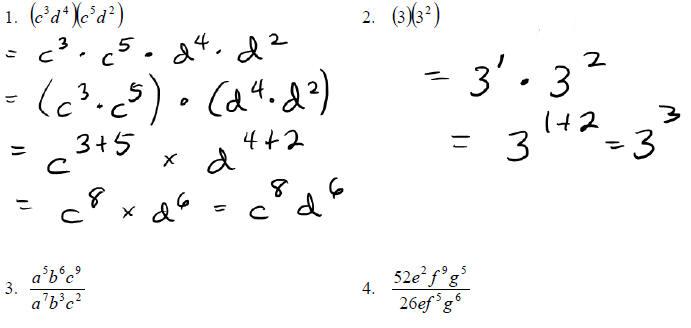



Different Ways of Expressing a Rational Number
Proper and Improper Fractions
PROPER FRACTION  IMPROPER FRACTION
IMPROPER FRACTION
Mixed Numbers
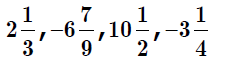
Decimals – Fractions meet the base ten number system
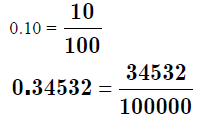
How do you turn a fraction into a decimal? Divide with
long division
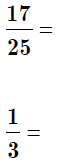
Repeating Decimals
Are RATIONAL NUMBERS!!
Notation:
An example of a decimal number that goes on forever but
does not repeat:
1.242442444244442444442444444...
Order and Rational Numbers
The expression x < y is equivalent to saying y – x > 0.
How to compare two rational numbers:
1. In Decimal Form
0.4443252 ____ 0.4433324
3.44 ____ 3.442
1003 _____ 1030
0.332 _____ 1.0004
2. In Fraction Form
a. Express both numbers as fractions – proper or improper
b. Find the common denominator
c. Express both fractions as equivalent fractions over the common
denominator.
d. Compare the numerators 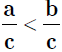 if and only if a <
b.
if and only if a <
b.
Practice:
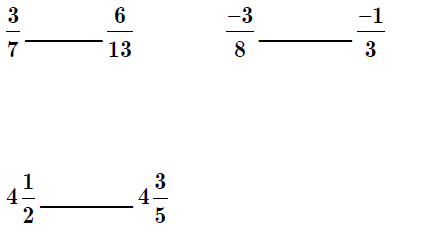
Summary: We now have the rational numbers, and we can
perform all four operations
with them and get a rational number answer. So, we have all the numbers we
need!!
OR DO WE???
Problem 1: Given a square with sides of length one inch,
how long is the diagonal?
Problem 2: Find the ratio of the circumference of a circle
to its diameter.
Neither of there two problems have answers that are
rational numbers!!
We need more numbers to describe REAL PHYSICAL LENGTHS.
Irrational Numbers are real numbers (real points on the
number line ) that CANNOT be
expressed as a ratio of two integers (fraction).
Examples: pi, the square root of 2, ..
We will work with square roots in this class. Other
classes will introduce you to other
irrational numbers.
Simplifying Radicals
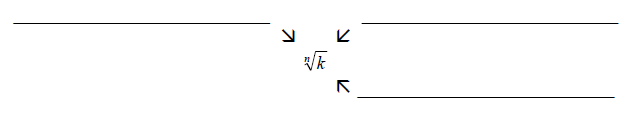
Note: When there isn’t a number for n, it means there’s really a 2 there.
Examples: