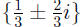Property 0.1 A few points to review.
• A quadratic equation in x can be written in the standard
form
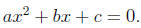
•Some equations can be solved by factoring .
•A polynomial function of the form
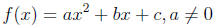
is a quadratic function . These are shaped like
bowls or inverted bowls.
• The real solutions of ax ^2 +bx+c = 0 correspond to the
x-intercepts for
the corresponding graph .
Property 0.2 If u is an algebraic expression and d
is a nonzero real number,
then u^2 = d is equivalent to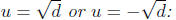 
Equivalently if u ^2 = d, then
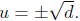
Note that we write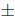 
as short hand for + and -. Whenever you
see 
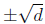
think of it as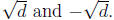 
Example 0.1 5x^2 = 20
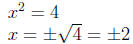means x = 2 or x =-2.
Check:
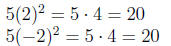
Example 0.2 4x^2 = 49
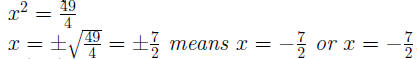
Check:
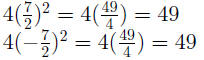
Example 0.3 4x^2 + 49 = 0
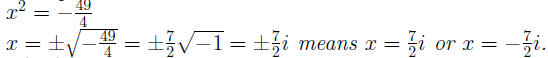
Check:
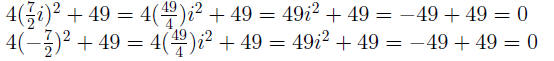
Example 0.4 (x-5)^2 =-4
Recall if u^2 = d, then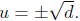
In this example u = (x-5) and d =-4.
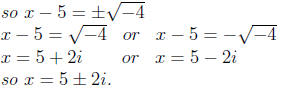
Property 0.3 If x^2 +bx is a binomial, then by
adding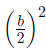 
which is the
square of half the coefficient of x, a perfect square trinomial will result.
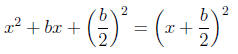
Whenever adding 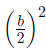to one
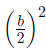side of the equation, make sure to add to
the other side as well.
Example 0.5 x^2 + 6x = 7
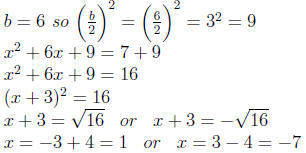
The solution set is {-7, 1}.
Example 0.6 x^2 + 8x - 5 = 0
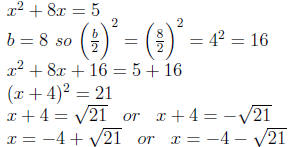
The solution set is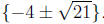 
If the coefficient of the x ^2 term is not equal to 1, then
divide the entire
equation by that coefficient.
Example 0.7 2x^2 + 5x - 3 = 0
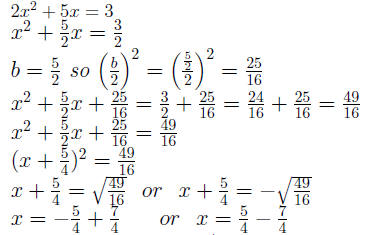
The solution set is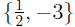 
Example 0.8 9x^2 - 6x + 5 = 0
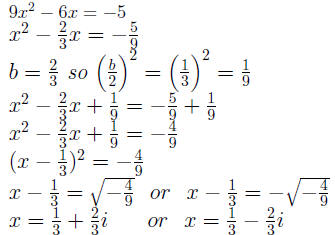
The solution set is 
