Properties of Rational Functions
p. 192: 17, 22, 24, 26, 30, 40, 41, 44, 48, 50, 51
17. To figure out the domain of R(x), we must only
calculate where x3 − 8 = 0. But now x3 − 8 = 0
x3 = 8 
x = 2. Thus our domain is
{x | x ≠ 2}.
22. To figure out the domain of F(x), we must calculate
where 3(x2+4x+4) = 0. But now 3(x2+4x+4) =
3(x + 2)2, so our domain is
{x | x ≠ −2}.
24. The graph of this function shows that
(a) Domain = (−∞,−1) ∪ (−1,∞) or {x | x ≠ −1}. Range =
(0,∞) or {y | y > 0}.
(b) No x- intercepts and y -intercept (0, 2)
(c) Horizontal asymptote y = 0.
(d) Vertical asymptote x = −1
(e) No Oblique asymptotes
26. The graph of this function shows that
(a) Domain = {x | x ≠ 0} Range = (−∞,−2) ∪ (2,∞) or {y | y
< −2 or y > 2}.
(b) No x- or y- intercepts
(c) No horizontal asymptote
(d) Vertical asymptote x = 0
(e) Oblique asymptote y = −x
30. Your graph should look something like :
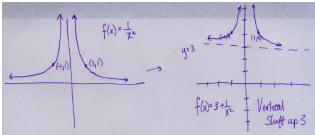
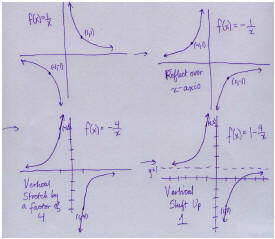
40. The trick here is noticing that
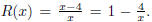Thus we can graph it using transformations,
getting something that looks like :
41. Let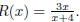 
The function
is already in lowest terms . Thus the vertical asymptotes are just where
the denominator is equal to zero,
x = −4.
To find the horizontal asymptotes, first note that our
function is not proper. Thus we must perform
long division to obtain
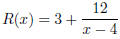
We thus get horizontal asymptote
y = 3
and no oblique asymptotes.
44. Let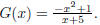 
We can factor
this as
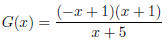
Which is already in lowest terms . Thus we find vertical
asymptote
x = −5.
To find the horizontal/oblique asymptote, note that the
function is not proper, so we must divide.
Long division yields
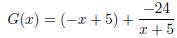
Which gives us oblique asymptote
y = −x + 5.
There are no horizontal asymptotes.
48. Let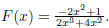 
Then we can
factor this as
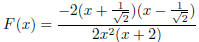
Thus our function is in lowest terms , and it follows that
our vertical asymptotes are
x = 0, x = −2.
Our function is proper in this case, so we get horizontal
asymptote
y = 0.
There are no oblique asymptotes.
50. Let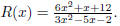 
Then we can
factor this function as
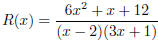
where the numerator is irreducible (Use the quadratic
formula to see this). Thus R(x) is in lowest
terms, and we get vertical asymptotes
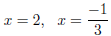
The function is not proper, so we must use long division
to see that
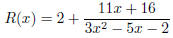
Thus
y = 2
Is the horizontal asymptote, and the function has no
oblique asymptotes.
51. Let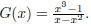 
Then we can
write
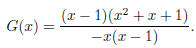
Our function is not in lowest terms . Thus, to find the
vertical asymptotes we must reduce :
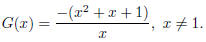
It follows that our only vertical asymptote is
x = 0.
Our function is not proper, so to find the horizontal or
oblique asymptotes we must use long division
to get
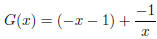
and thus we have oblique asymptote y = −x − 1. There are
no horizontal asymptotes.
