1. For each of the given (input, output) relationships in
Tables One and Two; answer the
following: Is the relationship a function? Why or why not?
a. A a function of B
b. B a function of A
c. C a function of D
d. D a function of C
For the relationships that are functions; also answer:
i. What is the domain of the function?
ii. What is the range of the function?
2. What is the domain and range for each of the following functions? Show your
work for
determining the domain when applicable. You may find graphing the function or
using the
calculator table feature for the function to be helpful; especially for
determining the range. If
you do so, include a sketch of the graph (label key points).
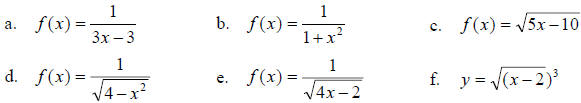
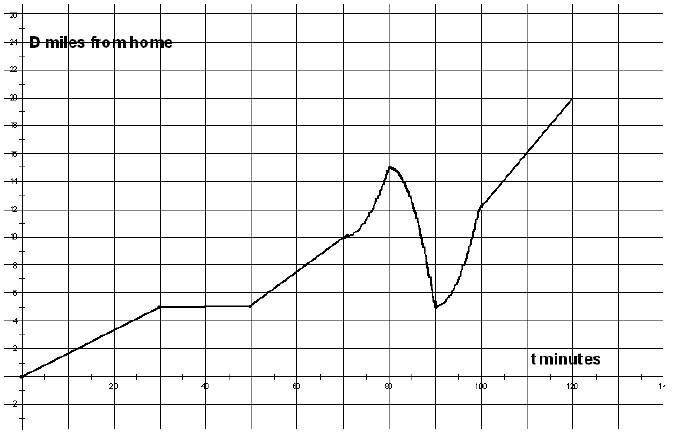
3. Use the provided graph of Eugene’s bike trip to answer
the following questions: Be sure you
can find equations of any of the requested lines.
a. When is Eugene taking a break? How do you know?
b. When is Eugene going away from or towards his house? How do you know?
c. When is Eugene going faster and faster? Explain how you know using calculus
concepts.
d. When is Eugene going slower and slower? Explain how you know using calculus
concepts.
e. When is Eugene going at a constant rate and what are his speeds in mph during
those
times ? Explain how you know using calculus concepts.
f. When is Eugene going the fastest and how fast, in mph is he going? Which
calculus
concept does this relate to?
g. What is Eugene’s average speed, in mph, during the first 45 minutes of his
trip? The
second 45 minutes? Which calculus concept does this relate to?
h. When is Eugene’s average speed 9 mph, 12 mph, 15 mph? Which calculus concept
does
this relate to?
i. When is Eugene’s speed 9 mph, 12 mph, 15 mph? Which calculus concept does
this
relate to?
MATH 495.595 / PRACTICE MIDTERM EUGENE’S BIKE TRIP
4. Suppose you wish to fence in a rectangular pen with 500
square feet of area with the front
and one side cedar fencing at $10 / foot and the back and the other side wire
fencing at $4 /
foot.
a. What is the least cost for such a rectangular pen? Support your conclusion
with a
carefully constructed cost function, a graph of the function with everything
clearly
labeled, with the least cost of the pen clearly marked on the graph and with a
final sketch
of the pen with the cost and the fence dimensions of the pen clearly labeled.
b. Suppose I wish to use the same construction ideas and spend exactly $1420 on
the
fencing material. What are the dimensions now? Use the quadratic formula for
full credit;
show your work for determining the solution ; mark the point(s) on the graph in
part a).
5. What is the open top box of maximum volume that can be made out of a 30 inch
by 50 inch
sheet of cardboard by cutting out corner squares and folding up the edges to
make a box as
we did in class? Construct a volume function and give all details of your
solution.
Graduate Only: Be sure you can multiply out the function and then use the
derivative rules
(power, constant multiple, sum) to also compute the derivative of the volume
function.
Describe the behavior of the volume function by comparing it to the derivative
function.
6. Suppose you wish to fence in a rectangular pen with 500 square feet of area
with the front
and one side cedar fencing at $10 / foot and the back and the other side wire
fencing at $4 /
foot.
a. What is the least cost for such a rectangular pen? Support your conclusion
with a
carefully constructed cost function, a graph of the function with everything
clearly
labeled, with the least cost of the pen clearly marked on the graph and with a
final sketch
of the pen with the cost and the fence dimensions of the pen clearly labeled.
b. Suppose I wish to use the same construction ideas and spend exactly $1420 on
the
fencing material. What are the dimensions now? Use the quadratic formula for
full credit;
show your work for determining the solution; mark the point(s) on the graph in
part a).
7. Use the Power , Constant Multiple and Sum Rules (as appropriate) to compute
the derivative
of a linear function . Explain your result in practical terms by describing the
relationship of
the result to the graph of the function.
8. Use Fermat’s Method to compute the derivatives of f (x) = 5x2 +1
and f (x) = 2 − x3 .
Carefully show all of your steps .
9. For each of the following, use the Power, Constant Multiple and Sum Rules (as
appropriate)
to determine f '(x) . Carefully show your work, don’t skip steps. Give your
answers without
negative exponents .
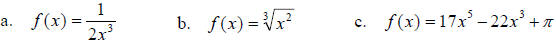
10. For each of the following functions, sketch the graph
of the derivative on the same axes.
Carefully mark all key points on the graphs and/or axes and explain your work.
Use key
terms in your explanations. Label your curves f (x) and f '(x)
Key Terms
| Function |
↑ , ↓, local max, local min, concave up, concave
down |
| Derivative |
> 0, < 0, = 0, ↑ , ↓ |
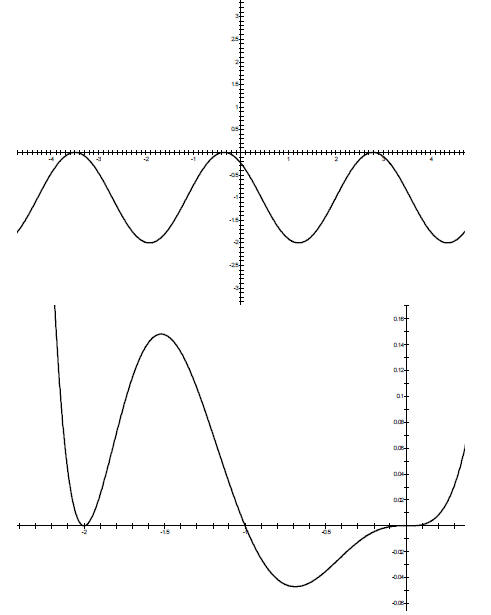
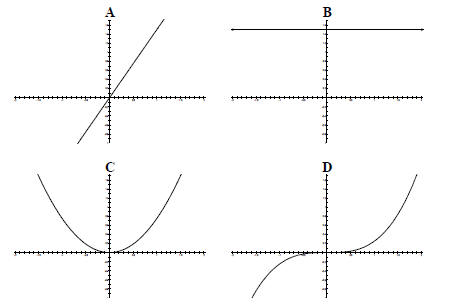
11. Identify as many relationships (graph A is the
derivative of graph _____ and the function for
graph ___, etc.) as possible. Explain your responses using key terms.
Key Terms
| Function |
↑ , ↓, local max, local min, concave
up, concave down |
| Derivative |
> 0, < 0, = 0, ↑ , ↓ |
12. Carefully sketch f (x) = x(x +1)(x −1) and then sketch
the graph of the derivative of f (x)
on the same axes. Carefully mark all key points on the graphs and/or axes and
explain your
work. Use key terms in your explanations. Label your curves f (x) and f '(x)



