1. Circle the graph that represents a function.
The correct graph is the second one. This is a piece-wise
defined func-
tion. The other two graphs fail the vertical line test.
2. Let
and 
.
Find the following functions
and state the domain of each:
a.) (f + g)(x)
Recall that (f + g)(x) is defined as f(x) + g(x). Therefore, to find
(f + g)(x), we add the given functions.
We have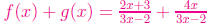
, which can be simplified to obtain
that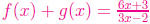 
.
Now, in order to find the domain , the rule is that the domain of
(f+g)(x) is the collection of all x values that are in BOTH the domain
of f and the domain of g. We need to make sure that neither function
has 0 in the denominator , so we set 3x−2 = 0 in order to solve for the
x -values that are NOT in the domain. This means that
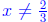is the
domain for both f and g, as well as for the function f + g.
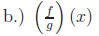
By definition,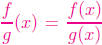 
, so
dividing the given functions, we have
that
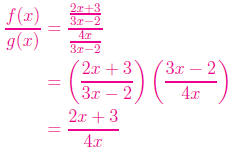
Now, when finding the domain, we must make sure that our
x-values
are still in BOTH the domain of f and the domain of g. We must also
make sure that g(x) ≠ 0. So, we still have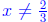
as found in part (a),
and we now have the additional restriction on our domain that
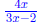
can’t be equal to 0. This means that x can not be equal to zero . Then,
the domain for this function is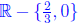 
, or simply x
≠ 0, and .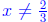
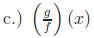
We are again dividing functions, this time dividing g by f. In this case,
the resulting function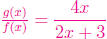 
.
To find the domain, we still need to have x values that are in both the
domain of f and the domain of g, so 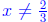is still
a requirement. Now,
we have to make sure that f(x) ≠ 0, so 2x + 3 can’t be 0. This means
that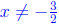 
, and the domain is
.
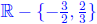3. Factor completely to simplify:
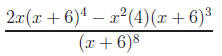
Remember, we are FACTORING, not expanding . To see the full so-
lution to this problem, please visit the factoring worksheet solutions
link.
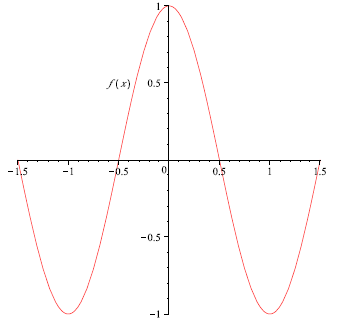
4. Use the graph of the above function to answer the
following:
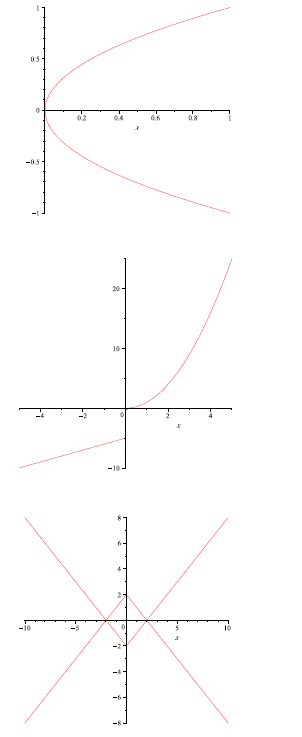
(a) Is f(x) even, odd, or neither?
This is an even function. We can tell by noticing that the graph
is symmetric about the y-axis. If you were to fold the page along
the x-axis, you’d notice that both halves of the graph lay perfectly
on top of one another. Alternatively, try to find some point x for
which f(x) and f(−x) are different . You could search forever, and
you’d never find one.
(b) Find f(1).
In order to find the value of f(1), we look for the y value when
x = 1. Since this y value is −1, we know that f(1) = −1.
(c) On which intervals is f(x) increasing?
As we move from left to right starting at x = −1, we notice that
the y values increase as the x values increase until we get to x = 0.
Therefore, we say that f(x) is increasing on the interval (−1, 0).
This also happens as we move from x = 1 to x = 1.5. So, the
function is also increasing on the interval (1, 1.5). Remember, we
never include the endpoints when talking about intervals on which
a function is increasing.
(d) What is the domain of f(x)?
There are no arrows on the graph to indicate that it continues
beyond the picture that we have on the page, so if we are look-
ing for the domain, we do not include any x values that are not
physically on the graph. Since there are no breaks in the graph or
open circles, we know that all x values shown are actually part of
the domain. Therefore, we can say that the domain is all values
of x such that −1.5 ≤ x ≤ 1.5. In interval notation, you would
write that the domain is [−1.5, 1.5].
(e) What is the range?
Again, there is nothing to indicate that the graph continues, so
we only include values based on the information given. Therefore,
since the y values on the graph range from −1 to 1 with no breaks,
we can say that the range of f(x) is all y values such that
−1≤ y ≤1. In interval notation, this is written as [−1, 1].
(f) At what numbers , if any, does f have a local maximum?
Notice that all points close to the point (0, 1) have lower y val -
ues. So, at x = 1, the function has a local maximum. The local
maximum value is 1.
(g) For which x values does f(x) = −1?
This is the same as asking for the x coordinates of any points on
the graph that have a y value of −1. Since the graph includes the
points (−1,−1) and (1,−1), we know that the x values for which
f(x) = −1 are x = −1 and x = 1.
