Lows of Logarithms

There are 3 basic laws for logarithms and
they each come from the three basic laws for
combining exponents .

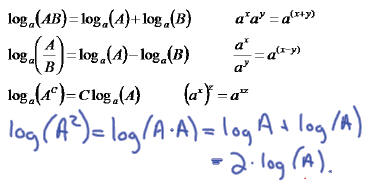
These are the common mistakes with
Logarithms. Watch for these.

There is often not much you can do to
simplify expressions like these (either the
left side or the right).

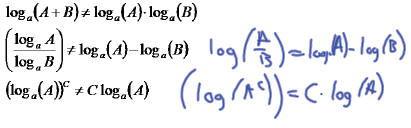
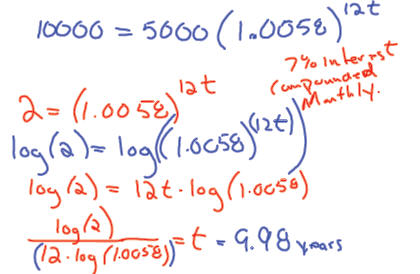
Examples of Simplifying : Combine into a
single (more complicated) log function .

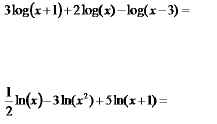
Change of Base Formula
It is often useful to change a logarithm to
either base ’10’ or base ‘e’.
To change 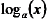into

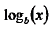
Start with

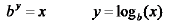
Take log base ‘a’ of both sides

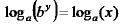
Solve for y

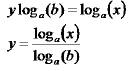
This gives the formula (usually used with
‘log’ or ‘ln’)

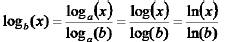
There is a similar way to change bases in
exponents.

Sec. 4.4 Exponential and Logarithmic
Equations

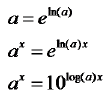
Guidelines for Solving Exponential Equations (page 359)
· Isolate the exponential expression on one side of the equation
· Take the logarithm of each side, then “bring down the exponent”
(which gets the variable out of the exponent )
· Use algebra to solve for the variable. And check your answer.

Guidelines for Solving Logarithmic Equations (page 362)
· Isolate the logarithmic expression on one side of the equation (you
may first need to combine the log terms )
· Raise the base to each side of the equation. (This gets rid of the log
function)
· Use algebra to solve for the variable . And check your answer.

Suppose the population of a small town is increasing at a rate of 5% each year.
In 2000, the population was 25,000 people.
Find a formula for the Population 't' years later.

What is the population today?

When will the population reach 100,000?

Examples

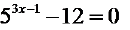
Examples of Exponential equations.

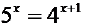
Examples. Try it two ways . First, get the exponential part by itself, then take logs.
Second. Take Logs to start and use Laws of Logarithms to simplify.

Examples of Logarithm Equations

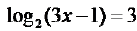
Examples.

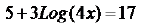
Examples.

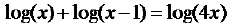
Hw Problems Sec. 4.3 Use the Laws of Exponents to Expand the Logarithm into several simpler ones.

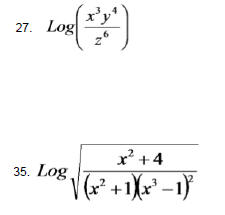
Hw Problems Sec. 4.3 Use the Laws of Exponents to combine the Logarithms.

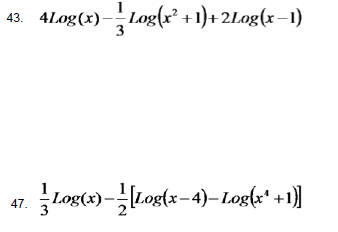
Hw Problems Sec. 4.4 Solve the following equations

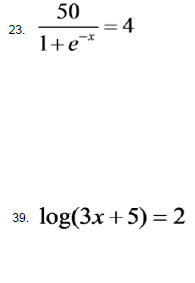
Hw Problems Sec. 4.4 Solve the following equations

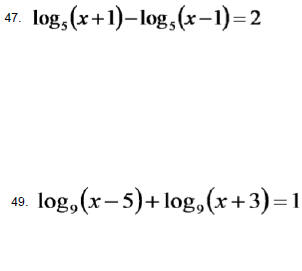
HW Problems:
69. Find the time required for an investment of $5000 to grow to $8000 at an interest rate of 7.5%
compounded quarterly .

HW 77. A small lake is stocked with fish. The population is modeled by the function

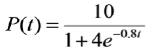
where P(t) is the population (in thousands) t years after the lake was stocked.
a) Find the population when t=0, when t= 3 and when t = 100 years.

b) After how many years will the population reach 5000 fish?