Maple is a computer algebra system primarily designed for the manipulation of
symbolic expressions. While the core functionality of Maple is similar to that
of Mathematica, the main advantage to Maple is a user friendly interface which
allows users to enter mathematical expressions as they would normally write
them.
1 Maple Basics
1.1 Entering Expressions
Maple has two main modes, command line and worksheet mode. The default
mode, worksheet, brings up a blank page where you can enter expressions by
typing the equation and evalute them by pressing enter . Maple input is the same
as you would write mathematically, so entering 2+3*5 would yield 17. (Note
that Maple does follow order of operations, however, if you want to make sure
expressions are evaluated in the correct order, use parenthesis. ex: 2+(3*5))
Default worksheet Maple does not require you to end a command with a
semicolon. You will only need to use a semicolon if you want to enter multiple
expressions on one line. 2*3;2*5 would output 6 and 10. If you want to supress
output, follow up the commands with a colon instead. 2*3:2*5: would evaluate
to the correct answers, but the results would not be shown (in this case, the
colon
defeats the point of the evaluation, but it can be useful for other operations).
By default, Maple evalutes numbers by using fractions . If you want a decimal
approximation, use evalf(number, digits), so evalf(Pi,5) would yield 3.1416.
You can also add a decimal after any number to force Maple to evalute as a
decimal . A third way is to right click on the output and select Approximate
followed by the number of digits you want to approximate to.
1.2 Variables and Functions
1.2.1 Variables
To assign a variable in Maple, enter the variable name followd be colon
equals
and then the variable value, so theta:=Pi would assign the variable θ a value
of . Note here that Pi is a reserved name by Maple equal to 3:14159 : : :. There
are a few other reserved names, but for the most part, variable names can be
just about anything that starts with a letter.
It is possible to assign almost anything to a variable, so entering
foo:=exp(I*x) would assign the variable foo a value of eix. (The imaginary
number, i is represented by I in Maple and is another reserved name and the
exponential function e is exp()) If we were to then enter eval(foo,x=theta),
Maple would output -1, since = 2*π from before, and eπi. (Euler's Identity)
Similarly assigning x:=theta and then entering foo would yield -1.
To clear a variable simply assign the variable its own
name in single quotes:
theta:=`theta'.
1.2.2 Functions
Functions in Maple are assigned by typing the function
name, colon equals
( variable(s) ) in function, right arrow, followed by the function. For example
f:=(x,y)->x^2+y would assign the function f such that f(x; y) = x^2+y. Then,
entering f(2,3), would evalute to 7.
1.3 Maple Commands
Maple has an extensive dictionary of commands. Each
command can be found
in the Maple documentation, along with examples and isntructions on how to
use a function. A list of useful commands can be found at the end of this
document.
2 Optimization in Maple
Maple hides most of its functionality in various packages.
To use these packages
enter with (packagename). A list of the functions contained within the package
will then be displayed. For optimization, use either the simplex package or the
Optimization package. Note that capitalization when loading a package does
matter.
Sometimes pacakges can contain several functions. If you
do not want to
see the output (in this case the list of packages), simply follow up the command
with a colon to supress output. This can avoid screen clutter.
Each function in Maple has a speci c syntax. Maple
contains extensive documentation
on all of its functions, which can be accessed through Help->Maple
Help or Ctrl + F1. Alternatively, you can enter ?commandnamehere to look up
the spec ed command name. (So ?int would bring up the help le for int)
2.1 The Simplex Package
First load the simplex package. with (simplex). A list of
the various functions
contained in the simplex package should be displayed. The two important ones
are maximize and minimize. Both take in a list of constraints and the objective
function. An example of using the maximize function is below. Minimize is
used in the same way.
> with ( simplex )
[ basis , convexhull , cterm , define_zero , display ,
dual , feasible , maximize , minimize , pivot ,
pivoteqn , pivotvar , ratio , setup , standardize ]
> obj := x1+2x2+4x3
x1+2*x2+4*x3
> constraints := {3x1+x2+5x3<=10,x1+4x2+x3<=8,2x1+2x3<=7}
{3*x1+x2+5*x3 <= 10 , x1+4*x2+x3 <= 8 , 2*x1+2*x3 <= 7}
> maximize ( obj , constraints ,NONNEGATIVE)
{x1 = 0 , x2 = 30/19 , x3 = 32/19}
Note that obj and constraints are simply variables, so you
could have just
entered them directly into maximize without rst assigning them.
2.2 The Optimization Package
The Optimization package works very similarly to the
simplex package, with
the main difference being the algorithm. The simplex package uses simplex to
optimize, while the Optimization package uses other more e cient algorithms.
> with ( simplex )
[ ImportMPS , Interactive , LPSolve , LSSolve , Maximize ,
Minimize , NLPSolve , QPSolve ]
> obj := x1+2x2+4x3
x1+2*x2+4*x3
> constraints :={3x1+x2+5x3<=10,x1+4x2+x3<=8,2x1+2x3<=7}
{3*x1+x2+5*x3 <= 10 , x1+4*x2+x3 <= 8 , 2*x1+2*x3 <= 7}
> maximize ( obj , constraints , assume=nonnegative )
[9.89473684210526 , [ x3 = 1.68421052631578937 , x1 = 0 . ,
x2 = 1.57894736842105265] ]
> convert (%, rational )
[188/19 , [ x3 = 32/19 , x1 = 0 , x2 = 30 / 19 ] ]
Note that % here refers to the previous output. Similarly,
%% would refer to the previous previous output, and so on. 188/19 is the value
of the objective function at the optimal point.
2.3 Interactive Solver
The interactive solver can be accessed through
Tools->Assistants->Optimization.... The interactive solver is easy to use,
just enter the objective function and then the constraints and hit solve. Note
that when entering expressions into the interactive solver you must explicity
write out all the multiplications ( unlike in worksheet Maple). For example,
write 5*x1+2*x2, and not 5x1+2x2.
The interactive solver also has an option to plot the
solution graphically up
to three variables.
To perform the majority of matrix operations first load
the linear algebra package
with (LinearAlgebra). The linalg package may also be used, but its commands
are different that the ones listed here, and is a deprecated package (which
is being phased out). Examples of using common linear algebra functions below.

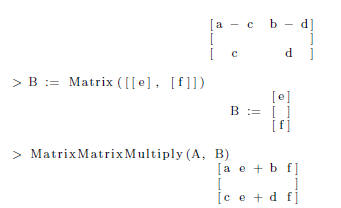
You may also use the Matrix editor in the left panel
( expand the matrix tab)
to insert a matrix. This is often easy to use, however, when multiplying
matrices ,
if you have a matrix with a dimension of 1 in either row or column,
Maple thinks it is a vector so you will need to use MatrixVectorMultiply or
VectorMatrixMultiply.
4 Useful Maple Commands
What follows is a list of some of the more useful commands
in Maple. Note that
commands can be nested within one another, so int (diff(x,x),x) would give
| > restart |
#resets all variables , unloads all packages |
| > eval ( x^2+2x+1,x=1) |
#evaluates the expression at x=1 |
| > evalf (Pi , 5) |
#evaluates the expression to 5 digits |
| > subs ( x=2x*y , x ^2) |
#subsitutes x=2*x*y into x^2 to give (2*x*y)^2 |
| > diff (5x*y , x ) |
#differentiates with respect to x |
| > diff (5x*y , x$2 ) |
#differentiates with respect to x twice
|
| > int ( sin ( x ) , x ) |
#integrates with respect to x |
| > int ( sin ( x )/x , x=0. . infinity ) |
#integrates from 0 to infinity to give Pi /2 |
| > simplify ( x*y+2*x*y-3*x ) |
#simplifies the expression ( this is really
useful ) |
| > expand ( ( x+1)(x+2)) |
#expands a factored expression |
| > factor ( x^2+2x+1) |
#factors an expression |
| > exp ( Pi*I ) |
#the exponentiale , function |
| > solve (5*x+x*y^2=3 ,x ) |
#solves the equation for x |
| > solve ({eq1 , eq2 , eq3 }, [ x , y , z ] ) |
#solves the system o f 3 eqs for x ,y ,and z |



