Functions

5. The Composition of Functions

Composition of two functions is a very fundamental and important
concept. If you think of a function as a calculation of some type, then,
roughly speaking, the composition of two functions, is the process
of calculating the value of one function , then based on that result,
calculate the value of the second function. The technical definition of
composition follows.

Let f and g be functions such that 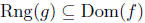 define f o g to
be a function whose domain is



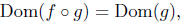
such that,



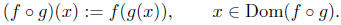
The function f o g is called the composition of f with g.

Compatible for Composition. Given a pair of functions, f and g,
if 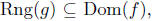we us agree to say that f is compatible with g
for composition.

Example 5.1. State the criterion under which the functions h is
compatible for composition with the function f. (That is, we wish to
compose h o f.)


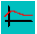
Figure 1

Figure 1 shows the Venn Diagram of the composition of
two functions. When thinking of composition, it is important
to visualize this picture. It often helps you to reason your way
through a difficult composition.

In terms of a black box interpretation we have the following diagram



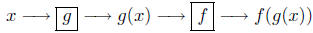
Example 5.2. Consider the two functions f(x) = sin(x) and g(x) =
x². (a) Is f compatible with g for composition? (b) Calculate the
domain of the composed function. (b) Compose f with g.

Multiple Compositions. Very often, functions of interest are, in
fact, the composition of several simple functions. The extension from
two function to three is obvious - at least after a few examples.

Example 5.3. Let f(x) = x⁵, g(x) = sin(x), and 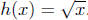Calculate
the function

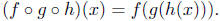
Exercise 5.1. Consider the functions

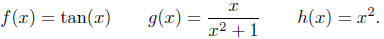
Calculate the composition 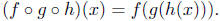Perform the
calculation two ways: In-to-Out, and Out-to-In.

The concept of composition is independent of the letters used to define
the functions and the variables.

Exercise 5.2. Consider the functions

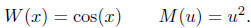
Calculate W o M and M o W.

Composition of Anonymous Functions. Very often, the functions
are given in anonymous form, say y = sin(x) and y = x². Now we
have a bit of a syntactical problem. How to explain to the user (you)
what we want to do. We could say, that we want to compose the first
function with the second function - until we reverse the order of
the functions , in which case we change our minds and now want to
compose the second with the first.

A popular convention is to relabel the variables so as to suggest our
intentions. Instead of writing y = sin(x) and y = x², write instead

y = sin(u) and u = x².

Does this now suggest our intention? The composition of the these
two functions is then

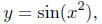
where now composition is reduced to a process of substitution of variables;
to tell you the truth, that's all composition is anyway.

Exercise 5.3. Consider the pair of functions w = s² + 2 and s =
t² - 1, compose these two functions together in the obvious order to
obtain w as a function of t.

A function may be the composition of three functions, four functions,
five functions, or any number of functions. If we label the variables
properly, multiple compositions is une 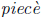du gateaux.

Example 5.4. Suppose y = u⁴, u = v² + 1, and v = sin(x). Perform
the implied composition
.
Actually, this relabeling of variables is sometimes used even when the
functions have names. In the abstract, we may describe two functions
by saying: define,

y = f(u) and u = g(x).

That is, f defines y as a function of u, and g defines u as a function of
x. Again, the choice of the variables suggests our intention to compose
f with g to get

y = f(g(x)),

the new function defines y as a function of x.

Composition and your Calculator. Composition of functions is an
operation you perform almost every time you use your hand-held calculator.
On your calculator, there is a series of buttons called function
keys. When you press two consecutive function keys on your calculator,
you are composing functions together.

For example, suppose you wanted to calculate the expression sin(x²),
for some particular number x. How would you do it? You would perform
a series of calculation steps. Step (1): Use the keypad to enter x
into the display. Step (2): Press the function key labeled x². Step (3):
Now press the function key labeled sin(x). You have just composed
functions! Here is a diagram of the sequence of operations:

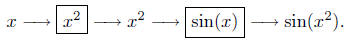
The " squaring box " squares whatever is input into its box, the "sine
box" take the sine of whatever is input into its box.

Now that I have amazed you with this observation, let me pop you
balloon. You don't actually have to press two function keys to compose
functions together. Consider the functions g(x) = x² + 2x + 3 and
f(x) = x². The composition of these two functions is

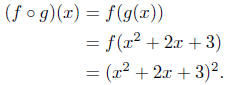	by defn of composition
	by defn of g
	by defn of f

To make this calculation on the calculator, we start with the initial
input value of x, some particular value. We then build up the expression
x² + 2x + 3 through a series of keypresses on our keypad,
utilizing the multiplication and addition buttons , as well as perhaps
the x² function key. Once we build up the value of x² + 2x + 3, then
we would press (possibly for a second time) the x² function key. This
key would then take the value in the display, which is x² +2x+3 and
square it. The process is diagramed as

As you can see, this process is indeed a composition: the output of a
function (x² + 2x + 3) is input back into another function x².

Patterns Observed. There is a pattern to composition that is important
that you be able to be aware of. To see the pattern let me
present a whole list of compositions, f o g, where, in each example,
the functions f is f(x) = sin(x), but the function g is different.

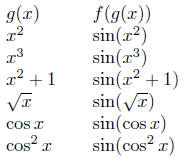
Let's do the same thing but with a different function f, say, f(x) = x³.
Repeating the above table with the new function f, we get.

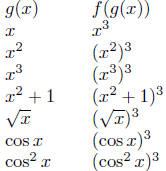
Of course, some of the entries in the second column can be simplified.
I left them that way so you could see the results of composition.

One more table. This one a little more abstract. Let the function
f(x) = (3x+1)⁴. Compose f with some functions of the form g(x) =
x + h, where h is an algebraic quantity (unspecified); or g(x) = ax,
where, again a is an algebraic quantity - plus variations on these
two.

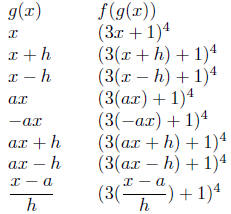
Have you gotten the "feel" for composition? As a rough rule, if you
want to compose a function f(x) = sin(x) with another function
g(x) = x² + 1, that is, if you want to compute the function f o g,
you take the "outer function," f in this case, and replace its "argument,"
that's x, with the value, g(x) of g, that's x². Thus,

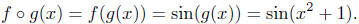
Uncomposing functions. In calculus, in order to perform certain
calculations on functions, it is important to analyze the function under
consideration. Part of that analysis is, perhaps, to realize that the
function you are studying can be thought of as the composition of
two other (simpler) functions. The importance of this ability to spot
composed functions cannot be overemphasized!

With the experience of the tables above, you should be able to solve
the following exercise without looking at the answer first.

Example 5.5. Consider the function 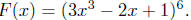Write
F as the composition of two other functions - let's call these two
functions f and g (That's original!).

Example 5.6. Consider the function F(x) = sin(1 + x³). Write f
as the composition of two other functions f and g; i.e. write F(x) =
f(g(x)).

The question a student might ask, if I permitted it, is how can this
decomposition be discerned? I might answer in any of three ways. (1)
Look at a large number of worked out examples, similar to the last example,
until you finally get a "feel" for the process, or see the pattern
of composition. Or, (2) Imagine how you would calculate the function
on your calculator - the consecutive pressing of function buttons.
Reread the discussion above. Or, (3) uncompose by substitution.

Uncompose by Substitution. The formal technique of substitution
is a way of uncomposing a function. Let me illustrate with a hideous
example:

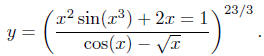
Isn't that ugly now? That base function o ends me! Let me mask it
over, or substitute it away. Let u be defined by

Now, my original function is not so bad; it becomes

where, u is the quantity defined in (1). What I have just done is
uncompose the hideous function into a non hideous part, 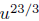, and
a semi-hideous part, (1).

What equations (2) and (1) represent is the implicit composition of
functions: define

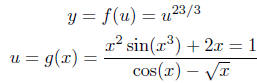
This substitution method is a very important tool used in differentiation
of complicated functions and in the integration of functions.

Exercise 5.4. Make an appropriate substitution of variables to help
you uncompose the function y = tan(x³ - 2x + 2).

6. Shifting and Rescaling

Let me divide the discussion into three topics: horizontal shifting,
vertical shifting, and rescaling.

Horizontal Shifting
Let y = f(x) be a function of a real variable, and let c > 0 be a
fixed constant. The graph of f is a certain curve in the xy -plane.
Sometimes we want to move the graph horizontally a distance of 'c.'
We may want to shift horizontally to the right or to the left.

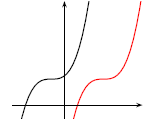
Figure 1

Shift Horizontally to the Right. define a new function
g (whose graph is going to be the graph of f shifted
over c units to the right) by



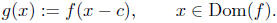
In Figure 1, the curve in red, the graph of g(x) =
f(x - c), is shifted c units to the right of the graph
of y = f(x), shown in black.

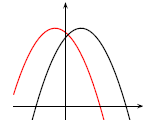
Figure 2

Shift Horizontally to the Left. define a new function
g (whose graph is going to be the graph of f shifted
over c units to the left) by



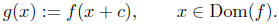
In Figure 2, the curve in red, the graph of g(x) =
f(x+c), is shifted c units to the left of the graph of
y = f(x), shown in black.

For those who want to know more. Decide in your own mind why
g(x) = f(x - c) shifts the graph c units to the right, here c > 0.
Explore through examples, perhaps on your graphing calculator.

Vertical Shifting
Let y = f(x) be a real-valued function, and let c > 0 be a fixed
constant. The graph of f is a certain curve in the xy-plane. Sometimes
we want to move the graph vertically a distance of 'c.' We may want
to shift vertically upward or downward.

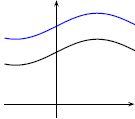
Figure 3

Shift Vertically Upwards. define a new function g
(whose graph is going to be the graph of f shifted
up c units) by



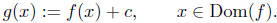
In Figure 3, the curve in blue, the graph of g(x) =
f(x) + c, is shifted c units upwards from the graph
of y = f(x), shown in black.

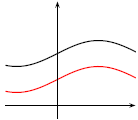
Figure 4

Shift Vertically Downwards. define a new function g
(whose graph is going to be the graph of f shifted
down c units) by



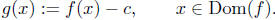
In Figure 4, the curve in red, the graph of g(x) =
f(x)-c, is shifted c units downwards from the graph
of y = f(x), shown in black.

Rescaling
Rescaling is a term taken from the applications this technique has
in many of the applied sciences. In the sciences, the variables of interested
are observable, perhaps measurable quantities. Quite often
the variables are measured in a certain scale of measurement: inches,
meters, pounds, liters, etc. Sometimes, it is desirable to change a relationship
from one scale of measurement to another: this is the origin
of the term.

Let y = f(x) be a function of a real variable, and let c be a fixed
constant (positive or negative). define a new function g by

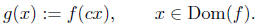
The constant c is sometimes called the scale factor .

For example, suppose a car travels at a constant speed of v = 55 mi/hr.
As we know, the distance traveled is given by d = vt = 55t, where
it is understood that t is measured in hours. Let's put this in functional
notation: d = f(t), where f(t) = 55t. Suppose now we want
to measure time in minutes. We still want to know the distance traveled,
but the input value, t, will be measured in seconds. Let u denote
time as measured in seconds; we know that u = 60t, or t = u/60.
(i.e. when t = 1, we want u = 60.) The distance function, now is
d = f(t) = f(u/60), or, more formally, define

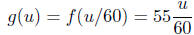
or,

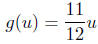
Let's make a calculation. After 6 minutes, how far has the car gone?

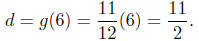
That is, the car has gone 5.5 miles.

7. Classification of Functions

A brief discussion some of the very common types of functions seen
in pure and applied mathematics. At this introductory level, we will
survey only the follow types at this time.

1. Polynomials.
2. Rational Functions.
3. Algebraic Functions.

Polynomial Functions
Let be define a polynomial function in a series of definitions.

Polynomial of degree 0. A polynomial of degree 0 is any function
of the form:



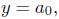
where a₀ is any constant. For example, y = 2 is considered a polynomial
of degree 0.

Polynomial of degree 1. A polynomial of degree 1 in x is any
function of the form.

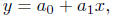
where a₀ and a₁ are constants. A polynomial of degree 1 is also called
a linear function. For example, y = 3+2x, or more commonly written,
y = 2x + 3 - this is a polynomial of degree 1 in x. A polynomial of
degree 1 in t might be y = 7t - 3.

Polynomial of degree 2. A polynomial of degree 2 in x is any
function of the form:

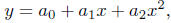
where a₀, a₁ and a₂ are constants - called the coefficients of the
polynomial. Such a polynomial is called a quadratic, meaning that it
is of degree 2. The graph, as you know is typically a parabola. A simple
example would be y = 1 + 2x + 2x²; this a polynomial of degree 2 in
x. Whereas, y = z² - 3z + 5 is a polynomial of degree 2 in z.

Polynomial of degree 3. A polynomial of degree 3 in x is any
function of the form:

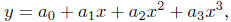
where a₀, a₁, a₂ and a₃ are constants (the coefficients of the polynomial).
Examples abound:


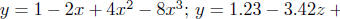
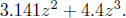
Polynomial of degree 4. A polynomial of degree 4 in x is any
function of the form:

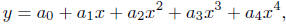
where a₀, a₁, a₂ ,a₃, and a₄ are constants (the coefficients of the
polynomial). Some examples would be y = x⁴ (the coefficients a₀ =
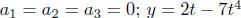, and so on.

The reason that I introduced polynomials in this rather monotonous
way is for you see them: see what they look like, see what they look
like relative to each other. As you can see, a polynomial of degree 2,
is a polynomial of degree 1 plus one additional term of higher power
(the x² term). Similarly, a polynomial of degree 3 is a polynomial of
degree 2 plus one additional term of higher power (the x³ term).

Here is a chart to drive home this point.

degree 0
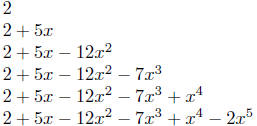degree 1
degree 2
degree 3
degree 4
degree 5

Let's tackle the general definition of a polynomial.

definition 7.1. Let n be a positive integer (n = 1, 2, 3,4, . . . ). A
polynomial of degree n in x is any function of the form:

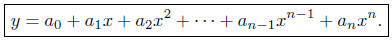
Where, as before, the symbols 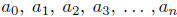are constants.
These constants are called the coefficients of the polynomial .

Domain Analysis: The natural domain of any polynomial is R, the
set of all real numbers.

More terminology: a₀ is referred to as the constant term; a₁ is the
coefficient of x (or is the coefficient of the degree 1 term); a₂ is the
coefficient of x²; a₃ is the coefficient of x³; and of course etc., etc., so
on and so forth.

More² terminology: If all the coefficients of a polynomial are integer,
we say that it is polynomial a polynomial with integer coefficients. For
example, 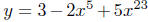is an polynomial with integer coefficients
in x of degree 23. If all the coefficients of a polynomial are rational
numbers, we say that it is a polynomial with rational coefficients. For
example, 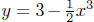is a polynomial with rational coefficients. What
do you think a polynomial with real coefficients is?
Exercise 7.1. Describe the function 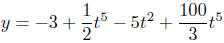using
the terminology of this section.

Exercise 7.2. Argue that any polynomial with rational coefficients
can be written as a rational scalar multiple of the polynomial with
integer coefficients.

Rational Functions
A rational function is any function that can be written as the quotient
of two polynomials. More technically,

definition 7.2. Let N(x) and D(x) be polynomials define a new
function r(x) by

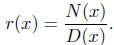
Domain Analysis: The natural domain of a rational function given by

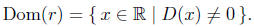
This analysis follows from the section on quotients of two functions.

Illustration 1. Here are some quick examples of rational functions:

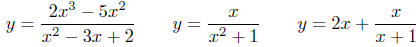
The latter example is considered a rational function of x since it can be
written as a quotient of two polynomial (get common denominator).

Algebraic Functions
Let's begin by setting the terminology.

definition 7.3. Analgebraic function in x is any combination of
sums, differences, products, quotients, and roots of x with itself and
with other constants (whether numerical or symbolic ).

Domain Analysis: The domain of an algebraic function is naturally
limited by the presence of even root functions and, of the function
consists of a ratio of two expressions, the presence of zeros in the
denominator .

Example 7.1. The following are algebraic functions. Do a domain
analysis of each.

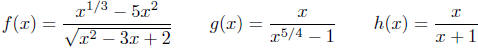
The last example is actually a rational function; however, it is true
that a rational function is also a algebraic function.