Part One
This game is intended to help you visualize what is going
on with fraction division . If you get lost at
any point in the program, you can scroll down the window for instructions.
You will be shown a point of the number line for which you
must enter the corresponding fraction. You must enter
the fraction in the form shown in the pictures below. The picture on the left
shows how you would enter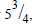 
and
the other picture shows 5. (Why is this 5?)
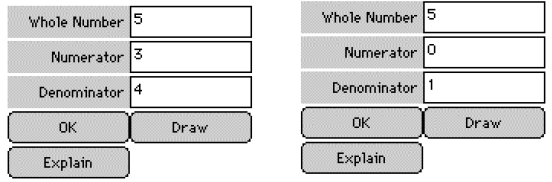
The number you have entered represents the dividend of
your division problem. Next, you will see a second
number line showing a new fraction- the divisor. You must now enter this number.
Finally, you must decide on
the answer (the quotient) and enter it. Click OK. Click DRAW to get a new
problem.
Play the game for at least 5 complete division problems.
Think about what it is that you are doing when you divide.
Write down your solution process for two of the problems
you solved. Include number line drawings like the ones
on the computer. Explain why the solution to each problem makes sense.
Part Two
Pretend that you were given these problems on the
computer:
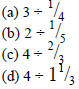
Create drawings for each problem to imitate what the
computer screen
would show. Explain in a sentence why the answer makes sense.
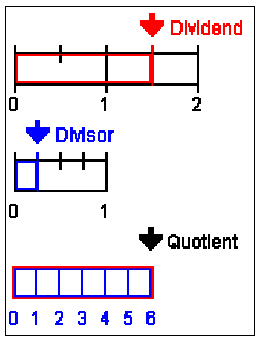
For example, the picture at right illustrates
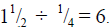This
makes sense because six one-fourths fit into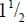 
.
Part Three
Most of you remember the “flip and multiply” algorithm for
dividing fractions :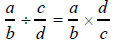
Why does this method work ? The purpose of this part of the
lab is to develop an understanding of why “flip and
multiply” works.
Example:
Wanda the Witch had 3 pounds of candy corn to give away at her Haunted House.
She decided to make 1/4 pound
bags to give away. How many bags of candy corn could she make?
(a) Let’s represent this story with a picture and use the
picture to determine the
answer.
Each rectangle represents 1 pound of candy corn. I divided
each pound into 4 equal regions to represent
1/4 pound bags. Now I can solve the problem by counting the number of 1/4ths in
the 3 pounds.
There are 12 1/4-pound bags in the 3 pounds of candy corn.
(b) Let’s write a division statement for this problem and
connect each number to the
problem .
Division statement: 3 ÷ 1/4. The 3 represents the whole: 3 pounds. The 1/4
represents the size of the
part that I am repeatedly taking away: 1/4 pound bags. So 3 pounds ÷ 1/4
pounds per bag = 12 bags.
(c) Let’s write a multiplication statement for this
problem and connect each number to
the problem.
Multiplication statement : 3 x 4. The 3 represents how many pounds of candy corn
Wanda has. The 4
represents the number of 1/4 pound bags that are in each pound of candy corn.
So 3 pounds x 4 bags per pound = 12 bags.
Explore the fraction division problems below by completing
steps (a)-(c) as illustrated in the
example above.
(1) A turtle undertakes a journey of 2 miles. Each day,
the turtle travels 1/5 of a mile. How many
days will it take the turtle to finish the journey?
(2) The Habitat for Humanity team can build 2/3 of a house
in one day. They plan to build 4
houses. How long will it take to finish all 4 houses?
(3) The vet has a new bottle containing 4 ounces of
special medicine. She will be administering
several doses of this medicine to her cats and dogs. Each dose is
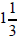ounces. How many doses
are in the bottle?
Look back at your solutions to the problems above. Write
an explanation for why it makes
sense to “flip and multiply” when you do fraction division.
