Review of Solving Radical
Equations
VOCABULARY & Properties
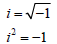
• Imaginary unit -- the number i
Note : This is used to take the square root of
negative numbers.
• Complex Numbers -- numbers of the form
a + bi (a is “ real ”, b is “imaginary”)
• Example: 2 + 3i or 4 - 7i
Review of Simplifying Radicals
Know the perfect squares : 1, 4, 9, 16, 25, 36, 49, 64, 81,
100, 121, 144, 169, 196, 225,…,400, 625, 900, 1000,…
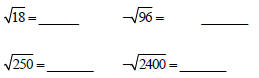
See Example 1, page 535
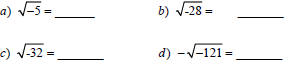
Because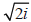 
and
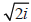are easily confused,
we usually write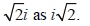 
Multiplication
When multiplying radicals with negatives, take
the root first, then multiply. Otherwise, you’ll
get the wrong answer.
taking root first vs. multiplying first
See Examples 2 & 3, page 540.
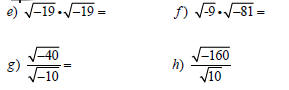
See Example 4, page 537.
To add or subtract , combine like terms.
• i) (3 + 5i ) + (2 - 4i )
• j) (4 - 6i ) - (3 - 7i )
• k) (9+i ) – (3 + 2i ) + (-5 – 3i )
For binomials , use the distributive property or
FOIL . (Don’t forget to substitute -1 for i^2.)
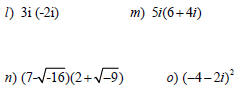
Complex Conjugates
• When dividing , we cannot leave a complex
number in the denominator.
• If the denominator is a binomial , multiply by its
conjugate to rationalize the denominator .
PRACTICE
Find the conjugate & multiply.
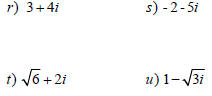
Divide.
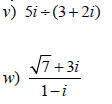
Summary
• Complex numbers standard form: a+bi
• To add or subtract , combine like terms.
• Simplify before multiplying.
• Always substitute -1 for i^2.
• Never leave an imaginary unit in the
denominator.
