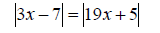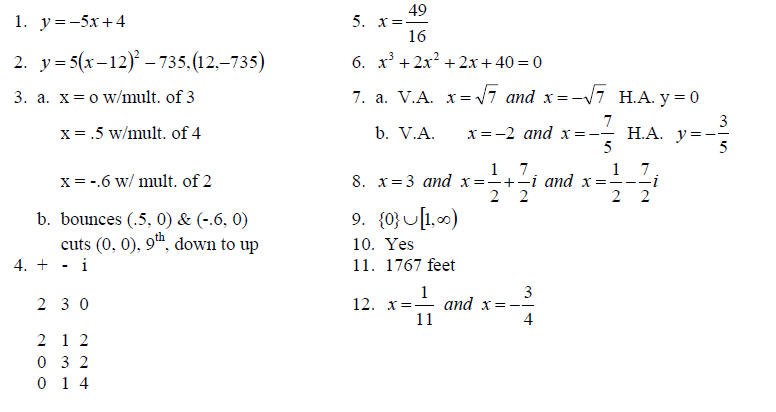1. Find the equation of the oblique asymptote for the
given rational function. (8 points)
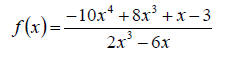
2. Write the quadratic equation in the form y = a(x − h)^2
+ k by using the completing the square method and
determine the vertex . All numbers should be in lowest term fractions or
integers . (8 points)
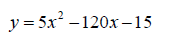
VERTEX IS__________________
3.
A. Find all possible zeros of the function and determine the multiplicity . (6
points)
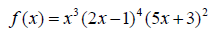
B. Using the same function from part A, state if a zero of
the function cuts or bounces at the x-axis,
determine the degree of the given polynomial function and determine the end
behavior. (5 points)
4. Build the table of all possible zeros for the
polynomial using Descartes ’ rule of signs . (8 points)
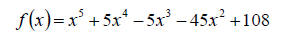
5. Solve the equation and check your answer. (10 points)
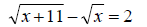
6. Find a polynomial equation with real coefficients that
has the given roots. (8 points)
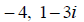
7. Find the equations of the vertical and horizontal
asymptotes for the given rational functions . (12
points)
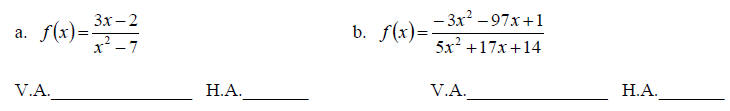
8. Determine all real and imaginary zeros of the
given function. Write answers as reduced fractions or
integers. (10 points)
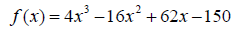
9. Solve the polynomial inequality using the test point
method. (10 points)
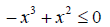
10. Determine if the given value is a zero of the function
using synthetic division . (7 points)
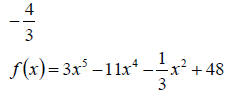
11. (6 points) If a soldier in basic training fires a
rocket propelled grenade (RPG) straight up from a height
of 3 feet with an initial velocity of 336 ft/sec, then its height above the
ground in feet at time t in seconds
is given by the function
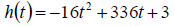
Do not round any of your calculations !
What is the maximum height reached by the RPG?
12. Solve the equation. Write answers in lowest term
fractions . (8 points)