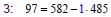Algorithm

Definition: An integer b is divisible by a
nonzero integer a if there is an integer c
such that ac = b.

Note: Saying that b is divisible by a is
equivalent to saying any of the following:
a is a divisor of b.
a divides b.
a is a factor of b.

Notation: aІb denotes that a divides b.

Theorem 1: For any  integers a, b, and c:

a. aІ0, 1Іa, and aІa.
b. aІ1 if and only if a = ±1.
c. If aІb and cІd, then acІbd.
d. If aІb and bІc, then aІc.
e. aІb and bІa if and only if a = ±b.
f. If aІb and aІc, then aІ(bx + cy) for any
integers x and y.

Some proofs of Theorem 1

Th 1a: aІ0, 1Іa, and aІa.

Recall: aІb <=> ac = b for some integer c.

Proof: a·0 = 0, 1·a = a, and a·1 = a.
So it follows from the def. of “is

a divisor of ” that aІ0, 1Іa, and aІa.

Th 1b: aІ1 if and only if a = ±1.

Proof: By the definition of “is a divisor of,”
aІ1 => ac = 1 for some integer c.
But the only integers whose product
is 1 are 1·1 and (-1)·(-1). So a = ±1.

On the other hand,
a = ±1 => a·(±1) = 1 => aІ1.

Th 1d: If aІb and bІc, then aІc.

Scratch work:
aІb and bІc => ap = b and bq = c
=> a(pq) = (ap)q = bq = c
=> aІc

Th 1d: If aІb and bІc, then aІc.

Proof: By the def. of “is a divisor of’” there
are integers p and q such that
aІb and bІc => ap = b and bq = c
=> a(pq) = (ap)q = bq = c

It now follows from the def. of “is a
divisor of that a Іc.

Th 1e: aІb and bІa if and only if a = ±b.

Sketch of Proof in one direction:

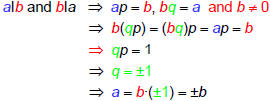
Greatest Common Divisor

d is the greatest common divisor of
integers a and b if d is the largest integer
which is a common divisor of both a and b.

Notation: d = gcd(a, b)

Example: ±2, ±7, and ±14 are the only
integers that are common divisors of both
42 and 56. Since 14 is the largest,
gcd(42, 56) = 14.

Use of the gcd

Reducing fractions

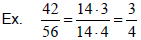
Not all fractions are easily reduced.

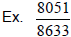
The Division Algorithm

For integers a and b, with b > 0, there
exist integers q and r such that

a = qb + r and 0 ≤ r < b.

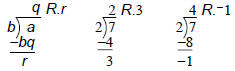
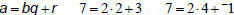
Euclidean Algorithm

To find gcd(a, b) where b < a:

Divide b into a and let r₁ be the remainder.
Divide r₁ into b and let r₂ be the remainder.
Divide r₂ into r₁ and let r₃ be the

remainder.
Continue to divide the remainder into the
divisor until you get a remainder of zero .

gcd(a, b) = the last nonzero remainder.

Find gcd(8633, 8051)

Theorem 2

For any nonzero integers a and b, there
exist integers x and y such that

gcd(a, b) = ax + by.

Here’s how you use the Euclidean
Algorithm to write gcd(8633, 8051) as a
linear combination of 8633 and 8051.

• Use the Euclidean Algorithm to find
gcd(8633, 8051).

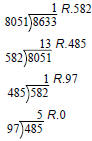
• Solve each division problem, except the
last one, for the remainder (r = a – bq) .
Take note of the quotient in each solution.

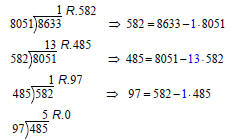
• Use these equations  
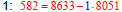
in reverse order to find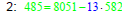
the linear combination .