This is a brief review of the most important stuff
covered in math 111. For detailed
explanation, refer to your notes and the handouts.
• Solving quadratic equations using quadratic formula
.
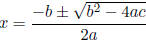• Absolute value equation. How to solve it? (Remember to check the answer for
absolute
value equations). For example, how to solve lx + 1l = -1?
• The equation of lines. x-intercept, y-intercept, when two lines are parallel ?
when two
lines are perpendicular?
• The distance between two points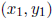 
and
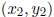is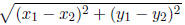 
• The equation of circles. Find the radius and center of the circle from given
equation.
• Given the graph of function f(x), how to find the x- intercept and y -intercept?
• Odd functions (f(-x) = -f(x)), even functions(f(-x) = f(x)). For example, f(x)
=
x4 + x, is it even, odd, neither or both?
• Piece-wisely defined function and the graph of it. (Take care with the
end-points)
• Functional notation. Composition of two functions.
• Inverse functions. Only the one to one functions have inverse functions.
• How to calculate the inverse function of f(x)? Let y = f(x), and solve for x.
• The domain of inverse function is just the range of the original function, and
the range
of inverse function is just the domain of the original function.
• The domain of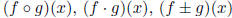 
and
.
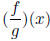• Difference quotient (what's the definition, how to calculate the difference
quotient?).
• The round-trip theorem: If g(x) is the inverse of f(x), then (f o g)(x)
= x and (g o f)(x) =
x. Example,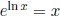 
and ln ex = x.
• Quadratic Function and its graph ( parabola ). The vertex of parabola . Given
quadratic
function f(x) = ax2 + bx + c, the parabola of its graph is
.
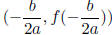• Use vertex to solve word problems (maximizing profit, sales-income, etc)
• If (x - a) is the factor of polynomial function f(x),
then f(a) = 0.
• Graph of polynomials. The leading item (the item with highest degree) totally
decides
the behavior of the graph at two ends (lxl is very big). The roots of polynomial
correspond
to the x-intercept of the graph. The multiplicity of each root (if multiplicity
is odd, then
the graph crosses the root, if multiplicity is even, then the graph touches the
root).
• Asymptotes and holes of rational functions.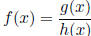 
, g(x) and h(x) are polynomials.
Solve for h(x) = 0. If the root (say, a) of h(x) = 0 satisfies g(a) ≠ 0, then x
= a is the
vertical asymptote. If a (the root of h(x) = 0) also satisfies g(a) = 0, and the
items
(x-a) can be canceled from the numerator and denominator , then x = a is a hole
of the graph of 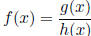. As for horizontal
asymptote, if g(x) and h(x) have the same
degree, then the horizontal asymptote is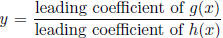 
. If
the degree of
g(x) is lower than the degree of h(x), then the horizontal asymptote is just y =
0 (the
x-axis). For example,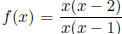
, then x = 0 is a hole
(because x can be canceled
from the numerator and denominator), x = 1 is a vertical asymptote, and y = 1 is
the
horizontal asymptote.
• Exponential functions . Domain and range of exponential functions. Graph of ex-
ponential functions (y-intercept). Word problems of exponential functions
(exponential
increase and exponential decrease. What's the beginning in the exponential in-
crease/decrease?).
• Logarithm functions (Read handouts for Sec5.3-5.4!). Domain of logarithm
functions.
Logarithm statement and exponential statement.
• Power law, product law and quotient law of logarithm functions. Solve
logarithm equa-
tions by trying to write the left side and right side of the equation into one
logarithm item.
For example: log (x - 1)+1 = -log x. How to solve
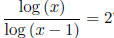? (Multiply log (x - 1)
on both sides first!) Don't forget to check your answer as the input for
logarithm
must be positive numbers!
• Solving equations for a variable in an exponent . For example,
,
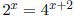just write 4 as
22, we get
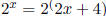(with the same base!), then x = 2x + 4. If the base is different,
say
,
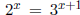just take natural logarithm on both sides and apply the power law for
logarithm, we get x ln 2 = (x + 1) ln 3, which is a linear equation !
•Word Problems. These problems are always interesting but not so
straightforward, review
the problems in your homework.
