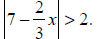Algebra Review

At Colorado State University, the College Algebra sequence extensively uses the graphing features of
the Texas Instruments TI-83 or TI-84 graphing calculator . Whenever possible, the questions on the
Math Placement Exam and in this review are designed to accommodate the student who has no
knowledge of these graphing features. However, students may find it helpful to learn about these
features.

POLYNOMIAL MANIPULATION

Polynomial expressions contain letters that symbolize numbers and obey the usual laws of arithmetic.
In adding, subtracting or multiplying polynomials , we apply these laws and combine like terms.

Example: Simplify the polynomial expression (x - 3)(2x + 5) - 6x(x - 1).
Solution:

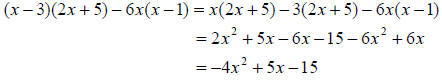
Problems:
1. Simplify: (3x - 7)(2x - 5) - x(4x - 3)
2. Simplify: (7x + 2)² - 5x[-3(x + 2)]
3. Simplify: (2x² - 5x + 3)(3x² + x - 2)
4. Simplify: 2(x + 3)³ - (x - 1)(x + 1)

SOLVING ONE LINEAR EQUATION IN ONE UNKNOWN

An equation (a statement equating two expressions ) can be manipulated by adding (or subtracting) the
same quantity from both sides, or by multiplying (or dividing) both sides by the same non- zero
quantity. To solve a simple linear equation we manipulate the equation into the form
Ax = B,

then divide by A to conclude that
x = B/A

Example: Solve for x in the following equation: 3(x - 2) - x = -5x - 4(2 - x).
Solution:
First perform all indicated multiplications: 3x - 6 - x = -5x - 8 + 4x.
Next simplify each side separately: 2x - 6 = -x - 8.
Now isolate all x terms on one side of the equation and all constant terms on the other
by adding x to both sides and adding 6 to both sides
3x = -2.

Divide by 3 to obtain the solution
x = -2/3

Problems:
5. Solve for x: 2(x + 4) = 5x - 12
6. Solve for u: -6[u - 4(u + 2)] = 5u - 4
7. Solve for R: 2R - 2(R + 3) = 4[2R - 3(1 + R)]

MATHEMATICAL MODELS

A mathematical model is a formula or algebraic equation that can be formed to model real-world
situations.

To model a real-world situation:
· Read the problem carefully. What information is given to you? What is the problem looking
for? Let x (or any variable ) represent one of the quantities of the problem.
· Write an expression with the information given.
· Evaluate the expression.
· Reread the problem. Does your answer make sense with the context of the problem?

Example: The length of the rectangular tennis court is 6 feet longer than twice the width. If the
court’s perimeter is 228 feet, what are the courts dimensions?

Solution: Let x = the width of the court. The length must be = 6 + 2x. We are given that the
perimeter = 228. The formula for perimeter is: 2W + 2L = P.

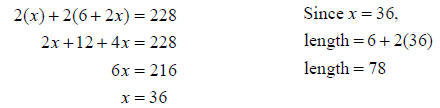
The dimensions of the tennis court are 36 ft. by 78 ft.

Problems:
8. For large parties, many restaurants automatically add an 18% gratuity to the bill. If the total bill,
including gratuity is $163.43, what was the bill before the gratuity was added?
9. A job pays an annual salary of $44,550, which includes a year-end bonus of $750. If paychecks
are issued twice a month, what is the gross amount of each paycheck?

INEQUALITIES/ABSOLUTE VALUES

Inequalities are manipulated in the same way as equalities with one notable exception. The direction
of the inequality changes when an inequality is multiplied or divided by a negative number. Such is
the case in the following:
8 > 3 so (-2)(8) < (-2)(3), since -16 < -6.

Example: Simplify the following: 2x + 5 ≥- x + 4.
Solution: Simplify the following: 2x + 5 ≥ -x + 4 .
Add x to both sides: 3x + 5 ≥4.

Subtract 5 from both sides, 3x ≥ -1, so that x ≥ -1/3.

Note that we divided by a positive number , therefore, no change in the inequality sign
occurs. The solution of an inequality is a set of numbers and can be graphed on the
number line . In the above example, the solutions are graphed as the (closed) half-line to
the right of -1/3 (inclusive).

Example: Simplify the following: -2x + 5 > x + 4.
Solution: Subtract x from both sides: -3x + 5 > 4.
Subtract 5 from both sides: -3x > -1.
Then x <1/3.

Note that we divided by a negative number; therefore, a sign change occurs in our
inequality. In this example, all x < 1/3 is graphed as the (open) half- line to the left of 1/3
excluding 1/3.

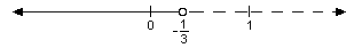
Problems:
10. Find the solution set of 5(x - 3) + 1 > -4(x - 1).
11. Find the solution set of -3x + 2 ≤ 5(2x + 3).
12. Find the solution set of

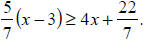
13. Find the solution set of (x + 2)(2x - 3) < 2(x + 1)(x + 5).
The absolute value of a number x is defined as

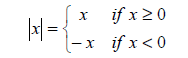
Hence, |5| = 5 and |-3| = 3. The absolute value of x can be visualized on a number line as the distance
the point x lies from the origin. Graphically we see that -3 is three units from the origin and 5 is five
units from the origin.

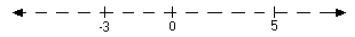
Example: Find the set of x-values satisfying |x| < 2.
Solution:
When x ≥ 0, |x| = x and the inequality becomes x < 2. Thus, the non-negative x-values
that satisfy |x| < 2 are given by 0 ≤ x < 2.
When x < 0, |x| = -x and the inequality becomes -x < 2, or -2 < x. Thus, the negative xvalues
that satisfy x < 2 are given by - 2 < x < 0 .
It follows that the set of all x-values satisfying |x| < 2 consists of all numbers x strictly
between -2 and 2 (excluding -2 and 2). The set of x-values satisfying |x| < 2, is the
collection of numbers within two units of the origin on the number line.

Example: Find the solution set of |2x - 1| < 3.
Solution:
Any solution of |2x - 1| < 3 must satisfy both of the inequalities 2x - 1 < 3 and
-3 < 2x - 1. These two inequalities can be written together as
-3 < 2x - 1 < 3
and then solved at the same time. Add 1 to all members of the inequality to get
-2 < 2x < 4. Divide by 2 to find that the solution set is the interval -1 < x < 2 of all
x-values strictly between -1 and 2.

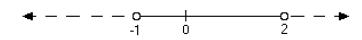
Problems:
14. Find the solution set of |6 - 2x| ≤ 3.
15. Find the solution set of

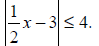
Example: Find the set of x-values satisfying |x| ≥ 2.
Solution:
When x ≥ 0, |x| = x and the inequality becomes x ≥ 2. Thus, the non-negative x- values
that satisfy |x| ≥2 are given by x ≥ 2.
When x < 0, |x| = -x and the inequality becomes -x ≥ 2, or x ≤ -2. Thus, the negative xvalues
that satisfy |x| ≥ 2 are given by x ≤ -2.
Thus, the set of all x-values satisfying |x| ≥2 is comprised of two disjoint sets. One set
is the real numbers x greater than or equal to 2. The other set is the real numbers x less
than or equal to -2. The set of x-values satisfying |x| ≥ 2 consists of the numbers two or
more units from the origin on the number line.

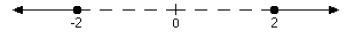
Example: Find the solution set of |2x - 1| ≥3.
Solution:
Any solution of |2x - 1| ≥ 3 must satisfy either the inequality 2x - 1 ≥ 3 or the inequality
2x - 1 ≤ -3. These two inequalities cannot be written together and should not be solvedat the same time.

When 2x – 1 ≥ 3,
2x ≥ 4,
so x ≥ 2

When 2x – 1 ≤ -3,
2x ≤ -2,
so x ≤ -1.

The solution set of |2x - 1| ≥ 3 is comprised of two pieces. One piece is the real
numbers x greater than or equal to 2. The other is the real numbers x less than or equal to -1.

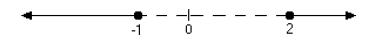
Notice that the solution set for |2x - 1| < 3 is an interval and the solution set for
|2x - 1| ≥ 3 is the complement of the same interval.

Problems:
16. Find the solution set of |5 - 2x| ≥ 3.
17. Find the solution set of